
【题目】在三棱柱ABC﹣A1B1C1中,CA=CB,侧面ABB1A1是边长为2的正方形,点E,F分别在线段AA1、A1B1上,且AE= ![]() ,A1F=
,A1F= ![]() ,CE⊥EF.
,CE⊥EF.
(Ⅰ)证明:平面ABB1A1⊥平面ABC;
(Ⅱ)若CA⊥CB,求直线AC1与平面CEF所成角的正弦值.
【答案】证明:(I)取AB的中点D,连结CD,DF,DE. ∵AC=BC,D是AB的中点,∴CD⊥AB.
∵侧面ABB1A1是边长为2的正方形,AE= ![]() ,A1F=
,A1F= ![]() .
.
∴A1E= ![]() ,EF=
,EF= 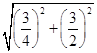 =
= ![]() ,DE=
,DE= 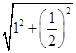 =
= ![]() ,
,
DF= 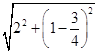 =
= ![]() ,
,
∴EF2+DE2=DF2 , ∴DE⊥EF,
又CE⊥EF,CE∩DE=E,CE平面CDE,DE平面CDE,
∴EF⊥平面CDE,又CD平面CDE,
∴CD⊥EF,
又CD⊥AB,AB平面ABB1A1 , EF平面ABB1A1 , AB,EF为相交直线,
∴CD⊥平面ABB1A1 , 又CDABC,
∴平面ABB1A1⊥平面ABC.
(II)∵平面ABB1A1⊥平面ABC,
∴三棱柱ABC﹣A1B1C1是直三棱柱,∴CC1⊥平面ABC.
∵CA⊥CB,AB=2,∴AC=BC= ![]() .
.
以C为原点,以CA,CB,CC1为坐标轴建立空间直角坐标系,如图所示: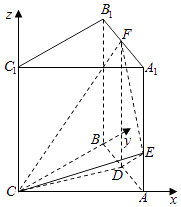
则A( ![]() ,0,0),C(0,0,0),C1(0,0,2),E(
,0,0),C(0,0,0),C1(0,0,2),E( ![]() ,0,
,0, ![]() ),F(
),F( ![]() ,
, ![]() ,2).
,2).
∴ ![]() =(﹣
=(﹣ ![]() ,0,2),
,0,2), ![]() =(
=( ![]() ,0,
,0, ![]() ),
), ![]() =(
=( ![]() ,
, ![]() ,2).
,2).
设平面CEF的法向量为 ![]() =(x,y,z),则
=(x,y,z),则 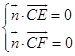 ,
,
∴ 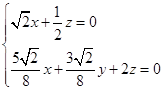 ,令z=4,得
,令z=4,得 ![]() =(﹣
=(﹣ ![]() ,﹣9
,﹣9 ![]() ,4).
,4).
∴ ![]() =10,|
=10,| ![]() |=6
|=6 ![]() ,|
,| ![]() |=
|= ![]() .
.
∴cos< ![]() >=
>= 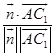 =
= ![]() .
.
∴直线AC1与平面CEF所成角的正弦值为 ![]() .
.
【解析】(I)取AB的中点D,连结CD,DF,DE.计算DE,EF,DF,利用勾股定理的逆定理得出DE⊥EF,由三线合一得CD⊥AB,故而CD⊥平面ABB1A1 , 从而平面ABB1A1⊥平面ABC;(II)以C为原点建立空间直角坐标系,求出 ![]() 和平面CEF的法向量
和平面CEF的法向量 ![]() ,则直线AC1与平面CEF所成角的正弦值等于|cos<
,则直线AC1与平面CEF所成角的正弦值等于|cos< ![]() >|.
>|.


科目:高中数学 来源: 题型:
【题目】点S、A、B、C在半径为 ![]() 的同一球面上,点S到平面ABC的距离为
的同一球面上,点S到平面ABC的距离为 ![]() ,AB=BC=CA=
,AB=BC=CA= ![]() ,则点S与△ABC中心的距离为( )
,则点S与△ABC中心的距离为( )
A.![]()
B.![]()
C.1
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)的图象是由函数g(x)=cosx的图象经过如下变换得到:先将g(x)的图象向右平移 ![]() 个单位长度,再将其图象上所有点的横坐标变为原来的一半,纵坐标不变,则函数f(x)的图象的一条对称轴方程为( )
个单位长度,再将其图象上所有点的横坐标变为原来的一半,纵坐标不变,则函数f(x)的图象的一条对称轴方程为( )
A.x= ![]()
B.x= ![]()
C.x= ![]()
D.x= ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
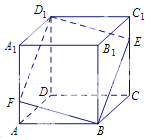
【题目】如图所示,在正方体![]() 中,点
中,点![]() 是棱
是棱![]() 上的一个动点,平面
上的一个动点,平面![]() 交棱
交棱![]() 于点
于点![]() .给出下列命题:
.给出下列命题:
①存在点![]() ,使得
,使得![]() //平面
//平面![]() ;
;
②对于任意的点![]() ,平面
,平面![]() 平面
平面![]() ;
;
③存在点![]() ,使得
,使得![]() 平面
平面![]() ;
;
④对于任意的点![]() ,四棱锥
,四棱锥![]() 的体积均不变.
的体积均不变.
其中正确命题的序号是______.(写出所有正确命题的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知关于x的不等式|x﹣2|﹣|x+3|≥|m+1|有解,记实数m的最大值为M.
(1)求M的值;
(2)正数a,b,c满足a+2b+c=M,求证: ![]() +
+ ![]() ≥1.
≥1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 已知数列
已知数列![]() 是递增的等比数列,a1+a4=9,a2a3=8,则数列
是递增的等比数列,a1+a4=9,a2a3=8,则数列![]() 的前n项和等于
的前n项和等于![]() ,解得a1=1,a4=8,或者a1=8,a4=1,但由于是递增数列,即a1=1,a4=8,即q3=
,解得a1=1,a4=8,或者a1=8,a4=1,但由于是递增数列,即a1=1,a4=8,即q3=![]() =8,所以q=2.因而数列
=8,所以q=2.因而数列![]() 的前n项和为 。
的前n项和为 。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方体ABCD—A1B1C1D1,

则下列四个命题:
①P在直线BC1上运动时,三棱锥A—D1PC的体积不变;
②P在直线BC1上运动时,直线AP与平面ACD1所成角的大小不变;
③P在直线BC1上运动时,二面角P—AD1—C的大小不变;
④M是平面A1B1C1D1上到点D和C1距离相等的点,则M点的轨迹是过D1点的直线D1A1。
其中真命题的编号是 。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com