
【题目】[选修4—5:不等式选讲]
已知函数![]() .
.
(1)当![]() 时,求不等式
时,求不等式![]() 的解集;
的解集;
(2)若不等式![]() 的解集包含
的解集包含![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)![]() ,或
,或 ![]() (Ⅱ)
(Ⅱ)![]() 或
或![]()
【解析】
试题分析:
(1)主要考查了含绝对值不等式的解法.当![]() 时,这里可采用零点分段法即可解出不等式的解集.(2)不等式
时,这里可采用零点分段法即可解出不等式的解集.(2)不等式![]() 的解集包含
的解集包含![]() ,易知当x∈[1,3]时,不等式f(x)≥|x﹣6|恒成立,适当变形为|x﹣a|≥|x﹣6|﹣|x﹣5|=6﹣x﹣(5﹣x)=1,即得|x﹣a|≥1在x∈[1,3]恒成立.
,易知当x∈[1,3]时,不等式f(x)≥|x﹣6|恒成立,适当变形为|x﹣a|≥|x﹣6|﹣|x﹣5|=6﹣x﹣(5﹣x)=1,即得|x﹣a|≥1在x∈[1,3]恒成立.
试题解析:
解:(1)当a=3时,求不等式f(x)≥3,即|x﹣3|+|x﹣5|≥3,
∴![]() ①,或
①,或 ![]() ②,或
②,或![]() ③.
③.
解①求得x≤![]() ;解②求得x∈
;解②求得x∈![]() ;解③求得x≥
;解③求得x≥![]() .
.
综上可得,不等式f(x)≥3的解集为{x|x≤![]() ,或 x≥
,或 x≥![]() }.
}.
(2)若不等式f(x)≥|x﹣6|的解集包含[1,3],
等价于当x∈[1,3]时,不等式f(x)≥|x﹣6|恒成立,
即|x﹣a|+|x﹣5|≥|x﹣6|恒成立,即|x﹣a|≥|x﹣6|﹣|x﹣5|=6﹣x﹣(5﹣x)=1恒成立,即|x﹣a|≥1 恒成立,
∴x﹣a≥1,或 x﹣a≤﹣1恒成立,即a≤x﹣1,或a≥x+1 恒成立,∴a≤0,或a≥4.
综上可得,a≤0,或a≥4.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:高中数学 来源: 题型:
【题目】我国是世界上严重缺水的国家,城市缺水问题较为突出,某市政府为了鼓励居民节约用水,计划在本市试行居民生活用水定额管理,即确定一个合理的居民月用水量标准:(单位:吨),用水量不超过![]() 的部分按平价收费,超过
的部分按平价收费,超过![]() 的部分按议价收费,为了了解全布市民用用水量分布情况,通过袖样,获得了100位居民某年的月用水量(单位:吨),将数据按照
的部分按议价收费,为了了解全布市民用用水量分布情况,通过袖样,获得了100位居民某年的月用水量(单位:吨),将数据按照![]() ……
……![]() 分成9组,制成了如图所示的频率分布直方图
分成9组,制成了如图所示的频率分布直方图

(1)求频率分布直方图中![]() 的值;
的值;
(2)若该市政府看望使85%的居民每月的用水量不超过标准![]() (吨),估计
(吨),估计![]() 的值,并说明理由。
的值,并说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() ,
,![]() 为参数),曲线
为参数),曲线![]() 上的点
上的点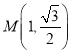 对应的参数
对应的参数![]() .在以O为极点,x轴的正半轴为极轴的极坐标系中,曲线
.在以O为极点,x轴的正半轴为极轴的极坐标系中,曲线![]() 是圆心在极轴上,且经过极点的圆.射线
是圆心在极轴上,且经过极点的圆.射线![]() 与曲线
与曲线![]() 交于点
交于点![]() .
.
(1)求曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若点![]() ,
,![]() 在曲线
在曲线![]() 上,求
上,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学名著《算法统宗》中有如下问题:“远望巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?”意思是:一座7层塔共挂了381盏灯,且相邻两层中的下一层灯数是上一层灯数的2倍,则塔的顶层共有灯( )
A. 1盏 B. 3盏 C. 5盏 D. 9盏
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着改革开放的不断深入,祖国不断富强,人民的生活水平逐步提高,为了进一步改善民生,2019年1月1日起我国实施了个人所得税的新政策,其政策的主要内容包括:(1)个税起征点为5000元;(2)每月应纳税所得额(含税)![]() 收入
收入![]() 个税起征点
个税起征点![]() 专项附加扣除;(3)专项附加扣除包括①赡养老人费用②子女教育费用③继续教育费用④大病医疗费用
专项附加扣除;(3)专项附加扣除包括①赡养老人费用②子女教育费用③继续教育费用④大病医疗费用![]() 等.其中前两项的扣除标准为:①赡养老人费用:每月扣除2000元②子女教育费用:每个子女每月扣除1000元.新个税政策的税率表部分内容如下:
等.其中前两项的扣除标准为:①赡养老人费用:每月扣除2000元②子女教育费用:每个子女每月扣除1000元.新个税政策的税率表部分内容如下:
级数 | 一级 | 二级 | 三级 | 四级 |
|
每月应纳税所得额(含税) | 不超过3000元的部分 | 超过3000元至12000元的部分 | 超过12000元至25000元的部分 | 超过25000元至35000元的部分 |
|
税率 | 3 | 10 | 20 | 25 |
|
(1)现有李某月收入29600元,膝下有一名子女,需要赡养老人,除此之外,无其它专项附加扣除.请问李某月应缴纳的个税金额为多少?
(2)为研究月薪为20000元的群体的纳税情况,现收集了某城市500名的公司白领的相关资料,通过整理资料可知,有一个孩子的有400人,没有孩子的有100人,有一个孩子的人中有300人需要赡养老人,没有孩子的人中有50人需要赡养老人,并且他们均不符合其它专项附加扣除(受统计的500人中,任何两人均不在一个家庭).若他们的月收入均为20000元,依据样本估计总体的思想,试估计在新个税政策下这类人群缴纳个税金额![]() 的分布列与期望.
的分布列与期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场举行有奖促销活动,顾客购买一定金额商品后即可抽奖,每次抽奖都从装有4个红球、6个白球的甲箱和装有5个红球、5个白球的乙箱中,各随机摸出1个球,在摸出的2个球中,若都是红球,则获一等奖;若只有1个红球,则获二等奖;若没有红球,则不获奖.
(1)求顾客抽奖1次能获奖的概率;
(2)若某顾客有3次抽奖机会,记该顾客在3次抽奖中获一等奖的次数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com