
【题目】某公司研发出一款产品,批量生产前先在某城市销售30天进行市场调查.调查结果发现:日销量![]() 与天数
与天数![]() 的对应关系服从图①所示的函数关系:每件产品的销售利润
的对应关系服从图①所示的函数关系:每件产品的销售利润![]() 与天数
与天数![]() 的对应关系服从图②所示的函数关系.图①由抛物线的一部分(
的对应关系服从图②所示的函数关系.图①由抛物线的一部分(![]() 为抛物线顶点)和线段
为抛物线顶点)和线段![]() 组成.
组成.
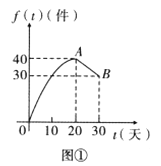
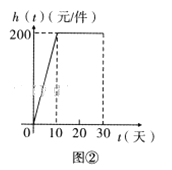
(Ⅰ)设该产品的日销售利润![]()
![]() ,分别求出
,分别求出![]() ,
, ![]() ,
, ![]() 的解析式,
的解析式,
(Ⅱ)若在30天的销售中,日销售利润至少有一天超过8500元,则可以投入批量生产,该产品是否可以投入批量生产,请说明理由.
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:高中数学 来源: 题型:
【题目】已知![]() ,
, ![]() 分别为等差数列和等比数列,
分别为等差数列和等比数列, ![]() ,
, ![]() 的前
的前![]() 项和为
项和为![]() .函数
.函数![]() 的导函数是
的导函数是![]() ,有
,有![]() ,且
,且![]() 是函数
是函数![]() 的零点.
的零点.
(1)求![]() 的值;
的值;
(2)若数列![]() 公差为
公差为![]() ,且点
,且点![]() ,当
,当![]() 时所有点都在指数函数
时所有点都在指数函数![]() 的图象上.
的图象上.
请你求出![]() 解析式,并证明:
解析式,并证明: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合M={f(x)|f2(x)﹣f2(y)=f(x+y)f(x﹣y),x,y∈R},有下列命题
①若f(x)= ![]() ,则f(x)∈M;
,则f(x)∈M;
②若f(x)=2x,则f(x)∈M;
③f(x)∈M,则y=f(x)的图象关于原点对称;
④f(x)∈M,则对于任意实数x1 , x2(x1≠x2),总有 ![]() <0成立;
<0成立;
其中所有正确命题的序号是 . (写出所有正确命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 和
和![]() 的通项公式分别为
的通项公式分别为![]() ,将集合
,将集合![]()
![]() 中的元素从小到大依次排列,构成数列
中的元素从小到大依次排列,构成数列![]() ;将集合
;将集合![]()
![]() 中的元素从小到大依次排列,构成数列
中的元素从小到大依次排列,构成数列![]() .
.
(1)求数列![]() 的通项公式
的通项公式![]() ;
;
(2)求数列![]() 的通项公式
的通项公式![]() ;
;
(3)设数列![]() 的前
的前![]() 项和为
项和为![]() ,求数列
,求数列![]() 的通项公式
的通项公式![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 ![]() 是定义在(﹣∞,+∞)上的奇函数,且满足
是定义在(﹣∞,+∞)上的奇函数,且满足 ![]()
(1)求实数a,b,并确定函数f(x)的解析式
(2)用定义证明f(x)在(﹣1,1)上是增函数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆C的中心为原点O,F(﹣2 ![]() ,0)为C的左焦点,P为C上一点,满足|OP|=|OF|且|PF|=4,则椭圆C的方程为( )
,0)为C的左焦点,P为C上一点,满足|OP|=|OF|且|PF|=4,则椭圆C的方程为( ) 
A.![]() =1
=1
B.![]() =1
=1
C.![]() =1
=1
D.![]() =1
=1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)是定义在R上的偶函数,且当x≤0时,f(x)=x2+2x.现已画出函数f(x)在y轴左侧的图象,如图所示,根据图象: 
(1)写出函数f(x),x∈R的增区间并将图象补充完整;
(2)写出函数f(x),x∈R的解析式;
(3)若函数g(x)=f(x)﹣4ax+2,x∈[1,3],求函数g(x)的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com