【题目】已知动圆 
经过点 
， 
.
（1）求周长最小的圆的一般方程；
（2）求圆心在直线 
上的圆的标准方程.
【答案】
（1）解：当AB为直径时，过A、B的圆的半径最小，从而周长最小．以AB中点(0,1)为圆心，半径r＝ 
|AB|＝ 
的圆的方程为x2＋(y－1)2＝10
（2）解：解法一：直线AB的斜率为k＝－3，则AB的垂直平分线的方程是y－1＝ 
x，即x－3y＋3＝0，由 
得 
即圆心是C(3,2)，所以半径r＝|AC|＝ 
，所以圆的方程是(x－3)2＋(y－2)2＝20.
解法二：设圆的方程为(x－a)2＋(y－b)2＝r2.
则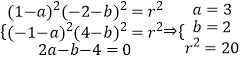 
所以圆的方程为(x－3)2＋(y－2)2＝20.
【解析】本题给出两个定点A、B，求经过AB周长最小的圆方程，并求圆心在定直线上的圆方程．
利用圆心到直线的d和半径r的关系判断． 圆心到直线的距离d.
①相交：d＜r,
②相切：d=r,
③相离：d＞r.
阅读快车系列答案科目：高中数学 来源： 题型：
【题目】对于数据3,3,2,3,6,3,10,3,6,3,2.
①这组数据的众数是3；
②这组数据的众数与中位数的数值不相等；
③这组数据的中位数与平均数的数值相等；
④这组数据的平均数与众数的值相等．
其中正确的结论的个数( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】观察下列各式： C 
=40；
C 
+C 
=41；
C 
+C 
+C 
=42；
C 
+C 
+C 
+C 
=43；
…
照此规律，当n∈N*时，
C 
+C 
+C 
+…+C 
= ．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】△ABC的三个顶点的坐标分别为A(1,0)，B(3,0)，C(3,4)，则△ABC的外接圆方程是( )
A.(x－2)2＋(y－2)2＝20
B.(x－2)2＋(y－2)2＝10
C.(x－2)2＋(y－2)2＝5
D.(x－2)2＋(y－2)2＝ 
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在三棱柱 
中， 
，底面三角形 
是边长为2的等边三角形， 
为 
的中点．
（1）求证： 
；
（2）若直线 
与平面 
所成的角为 
，求三棱柱 的体积．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】一个地区共有5个乡镇，共30万人，其人口比例为3∶2∶5∶2∶3，从这30万人中抽取一个300人的样本，分析某种疾病的发病率.已知这种疾病与不同的地理位置及水土有关，则应采取什么样的抽样方法?并写出具体过程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
