
【题目】已知函数![]() ,
,![]() 图象上两相邻对称轴之间的距离为
图象上两相邻对称轴之间的距离为![]() ;_______________;
;_______________;
(Ⅰ)在①![]() 的一条对称轴
的一条对称轴![]() ;②
;②![]() 的一个对称中心
的一个对称中心![]() ;③
;③![]() 的图象经过点
的图象经过点![]() 这三个条件中任选一个补充在上面空白横线中,然后确定函数的解析式;
这三个条件中任选一个补充在上面空白横线中,然后确定函数的解析式;
(Ⅱ)若动直线![]() 与
与![]() 和
和![]() 的图象分别交于
的图象分别交于![]() 、
、![]() 两点,求线段
两点,求线段![]() 长度的最大值及此时
长度的最大值及此时![]() 的值.
的值.
注:如果选择多个条件分别解答,按第一个解答计分.
【答案】(Ⅰ)选①或②或③,![]() ;(Ⅱ)当
;(Ⅱ)当![]() 或
或![]() 时,线段
时,线段![]() 的长取到最大值
的长取到最大值![]() .
.
【解析】
(Ⅰ)先根据题中信息求出函数![]() 的最小正周期,进而得出
的最小正周期,进而得出![]() .
.
选①,根据题意得出![]() ,结合
,结合![]() 的取值范围可求出
的取值范围可求出![]() 的值,进而得出函数
的值,进而得出函数![]() 的解析式;
的解析式;
选②,根据题意得出![]() ,结合
,结合![]() 的取值范围可求出
的取值范围可求出![]() 的值,进而得出函数
的值,进而得出函数![]() 的解析式;
的解析式;
选③,根据题意得出![]() ,结合
,结合![]() 的取值范围可求出
的取值范围可求出![]() 的值,进而得出函数
的值,进而得出函数![]() 的解析式;
的解析式;
(Ⅱ)令![]() ,利用三角恒等变换思想化简函数
,利用三角恒等变换思想化简函数![]() 的解析式,利用正弦型函数的基本性质求出
的解析式,利用正弦型函数的基本性质求出![]() 在
在![]() 上的最大值和最小值,由此可求得线段
上的最大值和最小值,由此可求得线段![]() 长度的最大值及此时
长度的最大值及此时![]() 的值.
的值.
(Ⅰ)由于函数![]() 图象上两相邻对称轴之间的距离为
图象上两相邻对称轴之间的距离为![]() ,则该函数的最小正周期为
,则该函数的最小正周期为![]() ,
,![]() ,此时
,此时![]() .
.
若选①,则函数![]() 的一条对称轴
的一条对称轴![]() ,则
,则![]() ,
,
得![]() ,
,![]() ,当
,当![]() 时,
时,![]() ,
,
此时,![]() ;
;
若选②,则函数![]() 的一个对称中心
的一个对称中心![]() ,则
,则![]() ,
,
得![]() ,
,![]() ,当
,当![]() 时,
时,![]() ,
,
此时,![]() ;
;
若选③,则函数![]() 的图象过点
的图象过点![]() ,则
,则![]() ,
,
得![]() ,
,![]() ,
,![]() ,
,
![]() ,解得
,解得![]() ,此时,
,此时,![]() .
.
综上所述,![]() ;
;
(Ⅱ)令![]()
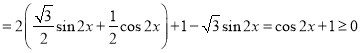 ,
,![]() ,
,
![]() ,
,![]() ,当
,当![]() 或
或![]() 时,即当
时,即当![]() 或
或![]() 时,
时,
线段![]() 的长取到最大值
的长取到最大值![]() .
.


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案科目:高中数学 来源: 题型:
【题目】已知数列{an}中,a1=1,a1+2a2+3a3+…+nan=![]() (n∈N*)
(n∈N*)
(Ⅰ)证明当n≥2时,数列{nan}是等比数列,并求数列{an}的通项an;
(Ⅱ)求数列{n2an}的前n项和Tn;
(Ⅲ)对任意n∈N*,使得![]() 恒成立,求实数λ的最小值.
恒成立,求实数λ的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为有效预防新冠肺炎对老年人的侵害,某医院到社区检查老年人的体质健康情况.从该社区全体老年人中,随机抽取12名进行体质健康测试,根据测试成绩(百分制)绘制茎叶图如下.根据老年人体质健康标准,可知成绩不低于80分为优良,且体质优良的老年人感染新冠肺炎的可能性较低.
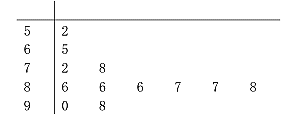
(Ⅰ)从抽取的12人中随机选取3人,记![]() 表示成绩优良的人数,求
表示成绩优良的人数,求![]() 的分布列及数学期望;
的分布列及数学期望;
(Ⅱ)将频率视为概率,根据用样本估计总体的思想,在该社区全体老年人中依次抽取10人,若抽到![]() 人的成绩是优良的可能性最大,求
人的成绩是优良的可能性最大,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修![]() :坐标系与参数方程选讲.
:坐标系与参数方程选讲.
在平面直角坐标系![]() 中,曲线
中,曲线![]() (
(![]() 为参数,实数
为参数,实数![]() ),曲线
),曲线![]()
![]() (
(![]() 为参数,实数
为参数,实数![]() ). 在以
). 在以![]() 为极点,
为极点, ![]() 轴的正半轴为极轴的极坐标系中,射线
轴的正半轴为极轴的极坐标系中,射线![]() 与
与![]() 交于
交于![]() 两点,与
两点,与![]() 交于
交于![]() 两点. 当
两点. 当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() .
.
(1)求![]() 的值; (2)求
的值; (2)求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,x
,x![]() R其中a>0.
R其中a>0.
(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)若函数f(x)在区间(-3,0)内恰有两个零点,求a的取值范围;
(Ⅲ)当a=1时,设函数f(x)在区间[t,t+3]上的最大值为M(t),最小值为m(t),记![]() ,求函数g(t)在区间[-4,-1]上的最小值.
,求函数g(t)在区间[-4,-1]上的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下是我们常见的空间几何体.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
(1) (2) (3) (4) (5) (6) (7) (8) (9)(10)
![]()
(11)
(1)以上几何体中哪些是棱柱?
(2)一个几何体为棱柱的充要条件是什么?
(3)如何求以上几何体的表面积?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com