
分析 根据函数f(x)=x2+ax+3的图象和性质,分析区间[1,3]与对称轴的关系,可得函数f(x)=x2+ax+3在[1,3]上的最大值.
解答 解:函数f(x)=x2+ax+3的图象是开口朝上,且以直线x=-$\frac{a}{2}$为对称轴的抛物线,
若-$\frac{a}{2}$≤$\frac{1+3}{2}$=2,即a≥-4,
则当x=3时,函数f(x)取最大值3a+9;
若-$\frac{a}{2}$>$\frac{1+3}{2}$=2,即a<-4,
则当x=1时,函数f(x)取最大值a+4;
点评 考查二次函数的对称轴的求解公式,二次函数的单调性,以及根据单调性求函数的最大值、最小值,根据取得顶点的情况或比较端点值来求二次函数最值的方法,要熟悉二次函数的图象


科目:高中数学 来源: 题型:选择题
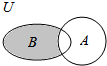 已知集合A={x|-$\sqrt{3}$≤x$\sqrt{3}$},B={x|-3≤x≤1},且A,B都是全集U的子集,则Venn图中阴影部分表示的集合为( )
已知集合A={x|-$\sqrt{3}$≤x$\sqrt{3}$},B={x|-3≤x≤1},且A,B都是全集U的子集,则Venn图中阴影部分表示的集合为( )| A. | {x|-$\sqrt{3}≤x≤1$} | B. | {x|-3≤x≤1} | C. | {x|-3$≤x≤-\sqrt{3}$} | D. | {x|1$≤x≤\sqrt{3}$} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com