
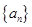 满足:
满足: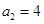 ,且对于任何
,且对于任何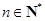 ,有
,有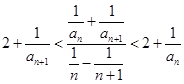 .
.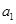 ,
,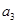 ;
;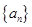 的通项
的通项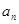 .
.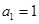 ,
,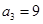 ;(2)
;(2)  .
.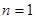 ,根据
,根据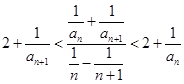 算得
算得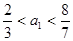 ,再根据
,再根据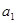 是正整数,算得.
是正整数,算得. 时,同样根据
时,同样根据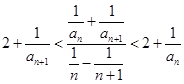 ,将
,将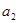 代入,得到
代入,得到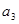 的范围,根据
的范围,根据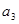 是正整数,求得
是正整数,求得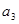 .
.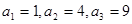 可猜想
可猜想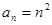 ,再用数学归纳法证明.
,再用数学归纳法证明.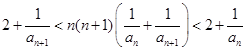 ①
①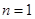 时,由
时,由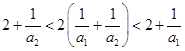 ,即有
,即有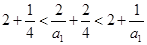 ,
,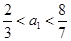 .因为
.因为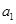 为正整数,故
为正整数,故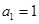 .
.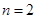 时,由
时,由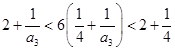 ,
,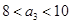 ,所以
,所以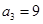 .
.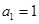 ,
,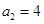 ,
,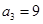 ,猜想:
,猜想: .
. 当
当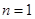 ,
,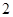 时,由(1)知
时,由(1)知 均成立;
均成立; 假设
假设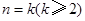 成立,则
成立,则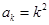 ,则
,则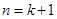 时
时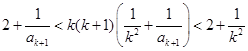
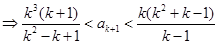
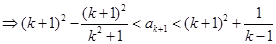
 时,
时,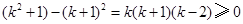 ,所以
,所以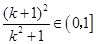 .
.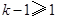 ,所以
,所以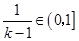 .
.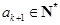 ,所以
,所以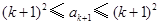 .
.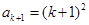 ,即
,即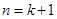 时,
时, 成立.
成立. ,2
,2 知,对任意
知,对任意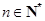 ,
, .
.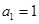 ,
,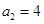 ,
,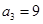 ,猜想:
,猜想: .
. 当
当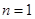 ,
,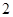 时,由(1)知
时,由(1)知 均成立;
均成立; 假设
假设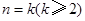 成立,则
成立,则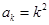 ,则
,则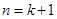 时
时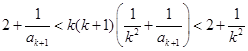
 ②
②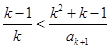 ,即
,即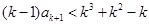 ,因为两端为整数,
,因为两端为整数, .于是
.于是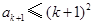 ③
③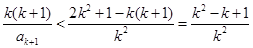 .
.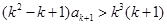 .
.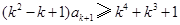 ,
,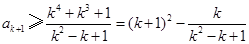 .
. 时,
时,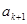 为正整数,则
为正整数,则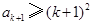 ④
④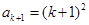 ,即
,即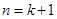 时,
时, 成立.
成立. ,2
,2 知,对任意
知,对任意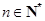 ,
, .
.

 发散思维新课堂系列答案
发散思维新课堂系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com