[题目]已知AD与BC是四面体ABCD中相互垂直的棱.若AD=BC=6.且∠ABD=∠ACD=60°.则四面体ABCD的体积的最大值是( )A.B.C.18D.36 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】已知AD与BC是四面体ABCD中相互垂直的棱，若AD=BC=6，且∠ABD=∠ACD=60°，则四面体ABCD的体积的最大值是（）
A.
B.
C.18
D.36

【答案】A
【解析】解：过C作CF⊥AD，垂足为F，连接BF，

∵BC⊥AD，CF⊥AD，BC∩CF=C，

∴AD⊥平面BCF，

∴VA﹣BCD= S△BCFAD=2S△BCF．

又∠ACD=∠ABD，AD⊥平面BCF，

∴△ACD≌△ABD，∴CF=BF，

取BC的中点E，则EF⊥BC，

∴2S△ADE=2× ×BC×EF=6EF，

∴当EF最大时，棱锥的体积取得最大值．

又EF= = ，故当CF最大时，棱锥体积最大，

∵∠ACD=60°，AD=6，∴当AC=CD时，CF取得最大值，

此时CF= =3 ，∴EF=3

∴棱锥的体积最大值为6EF=18 ．

故选A．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】各项均为非负整数的数列{an}同时满足下列条件： ①a1=m（m∈N*）；②an≤n﹣1（n≥2）；③n是a1+a2+…+an的因数（n≥1）．
（Ⅰ）当m=5时，写出数列{an}的前五项；
（Ⅱ）若数列{an}的前三项互不相等，且n≥3时，an为常数，求m的值；
（Ⅲ）求证：对任意正整数m，存在正整数M，使得n≥M时，an为常数．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】平面直角坐标系xOy中，过椭圆M： =1（a＞b＞0）焦点的直线x+y﹣2 =0交M于P，Q两点，G为PQ的中点，且OG的斜率为9．
（1）求M的方程；
（2）A、B是M的左、右顶点，C、D是M上的两点，若AC⊥BD，求四边形ABCD面积的最大值．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】我国古代的天文学和数学著作《周髀算经》中记载：一年有二十四个节气，每个节气晷（guǐ）长损益相同（晷是按照日影测定时刻的仪器，晷长即为所测量影子的长度）．二十四节气及晷长变化如图所示，相邻两个节气晷长的变化量相同，周而复始．若冬至晷长一丈三尺五寸，夏至晷长一尺五寸（一丈等于十尺，一尺等于十寸），则夏至之后的那个节气（小暑）晷长是（）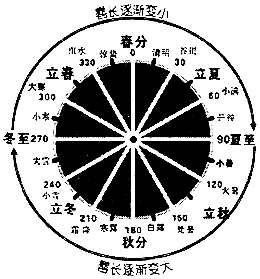
A.五寸
B.二尺五寸
C.三尺五寸
D.四尺五寸

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】在平面直角坐标系xOy中，以坐标原点为极点，x轴的非负半轴为极轴建立极坐标系，已知曲线C的极坐标方程为ρ=2 cos（ ﹣θ）
（1）求曲线C的直角坐标方程；
（2）已知直线l过点P（1，0）且与曲线C交于A，B两点，若|PA|+|PB|= ，求直线l的倾斜角α．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知过抛物线E：x2=2py（p＞0）焦点F且倾斜角的60°直线l与抛物线E交于点M，N，△OMN的面积为4．
（1）求抛物线E的方程；
（2）设P是直线y=﹣2上的一个动点，过P作抛物线E的切线，切点分别为A、B，直线AB与直线OP、y轴的交点分别为Q、R，点C、D是以R为圆心、RQ为半径的圆上任意两点，求∠CPD最大时点P的坐标．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】对于集合，定义了一种运算“ ”，使得集合中的元素间满足条件：如果存在元素，使得对任意，都有，则称元素是集合对运算“ ”的单位元素．例如：，运算“ ”为普通乘法；存在，使得对任意，都有，所以元素是集合对普通乘法的单位元素．
下面给出三个集合及相应的运算“ ”：
② ，运算“ ”为普通减法；
② 表示阶矩阵， }，运算“ ”为矩阵加法；
③ （其中是任意非空集合），运算“ ”为求两个集合的交集．
其中对运算“ ”有单位元素的集合序号为（）
A.①②；
B.①③；
C.①②③；
D.②③．