
【题目】设向量 ![]() =(sin
=(sin ![]() x,cos
x,cos ![]() x),
x), ![]() =(sin
=(sin ![]() x,
x, ![]() sin
sin ![]() x),x∈R,函数f(x)=
x),x∈R,函数f(x)= ![]() ,求:
,求:
(1)f(x)的最小正周期;
(2)f(x)在区间[0,1]上的最大值和最小值,以及取得最大值和最小值时x的值.
【答案】
(1)解:∵ ![]() =(sin
=(sin ![]() x,cos
x,cos ![]() x),
x), ![]() =(sin
=(sin ![]() x,
x, ![]() sin
sin ![]() x),x∈R,
x),x∈R,
∴f(x)= ![]()
=(sin ![]() x,cos
x,cos ![]() x)(3sin
x)(3sin ![]() x,cos
x,cos ![]() x+2
x+2 ![]() sin
sin ![]() x)
x)
=3sin2 ![]() x+(cos
x+(cos ![]() x+2
x+2 ![]() sin
sin ![]() x)cos
x)cos ![]() x
x
= ![]() sinπx﹣cosπx+2
sinπx﹣cosπx+2
=2sin(πx﹣ ![]() )+2,
)+2,
∴f(x)的最小正周期为T= ![]() =2
=2
(2)解:∵x∈[0,1],∴πx﹣ ![]() ∈[﹣
∈[﹣ ![]() ,
, ![]() ],
],
∴sin(πx﹣ ![]() )∈[﹣
)∈[﹣ ![]() ,1];
,1];
当πx﹣ ![]() =﹣
=﹣ ![]() ,即x=0时,f(x)取得最小值为2×(﹣
,即x=0时,f(x)取得最小值为2×(﹣ ![]() )+2=1,
)+2=1,
当πx﹣ ![]() =
= ![]() ,即x=
,即x= ![]() 时,f(x)取得最大值为2×1+2=4
时,f(x)取得最大值为2×1+2=4
【解析】(1)由平面向量的数量积运算,利用三角函数的恒等变换化简f(x),即可求出f(x)的最小正周期;(2)根据x∈[0,1],利用正弦函数的图象与性质,即可求出f(x)的最值以及对应的x的取值.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,菱形ABCD的边长为2,△BCD为正三角形,现将△BCD沿BD向上折起,折起后的点C记为C′,且CC′= ![]() ,连接CC′,E为CC′的中点.
,连接CC′,E为CC′的中点. 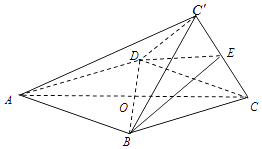
文科:
(1)求证:AC′∥平面BDE;
(2)求证:CC′⊥平面BDE;
(3)求三棱锥C′﹣BCD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() ,
, ![]() ),
),![]() (
(![]() ),且
),且![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() .
.
(Ⅰ)求![]() ,
, ![]() 的值;
的值;
(Ⅱ)若函数![]() 在区间
在区间![]() 内有且仅有一个极值点,求
内有且仅有一个极值点,求![]() 的取值范围;
的取值范围;
(Ⅲ)设![]() (
(![]() )为两曲线
)为两曲线![]() (
(![]() ),
),![]() 的交点,且两曲线在交点
的交点,且两曲线在交点![]() 处的切线分别为
处的切线分别为![]() ,
, ![]() .若取
.若取![]() ,试判断当直线
,试判断当直线![]() ,
, ![]() 与
与![]() 轴围成等腰三角形时
轴围成等腰三角形时![]() 值的个数并说明理由.
值的个数并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知如图所示的程序框图 
(1)当输入的x为2,﹣1时,分别计算输出的y值,并写出输出值y关于输入值x的函数关系式;
(2)当输出的结果为4时,求输入的x的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了增强市民的环境保护组织,某市面向全市征召n名义务宣传志愿者,成立环境保护宣传组织,现按年龄把该组织的成员分成5组:[20,25),[25,30),[30,35),[35,40),[40,45]. 得到的频率分布直方图如图所示,已知该组织的成员年龄在[35,40)内有20人 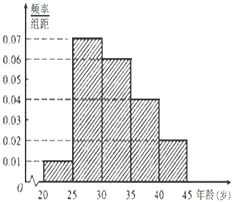
(1)求该组织的人数;
(2)若从该组织年龄在[20,25),[25,30),[30,35)内的成员中用分层抽样的方法共抽取14名志愿者参加某社区的宣传活动,问应各抽取多少名志愿者?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个命题中,正确的有( ) ①两个变量间的相关系数r越小,说明两变量间的线性相关程度越低;
②命题“x∈R,使得x2+x+1<0”的否定是:“对x∈R,均有x2+x+1>0”;
③命题“p∧q为真”是命题“p∨q为真”的必要不充分条件;
④若函数f(x)=x3+3ax2+bx+a2在x=﹣1有极值0,则a=2,b=9或a=1,b=3.
A.0 个
B.1 个
C.2 个
D.3个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有甲、乙两个靶.某射手向甲靶射击一次,命中的概率为 ![]() ,命中得1分,没有命中得0分;向乙靶射击两次,每次命中的概率为
,命中得1分,没有命中得0分;向乙靶射击两次,每次命中的概率为 ![]() ,每命中一次得2分,没有命中得0分.该射手每次射击的结果相互独立.假设该射手完成以上三次射击. (Ⅰ)求该射手恰好命中一次得的概率;
,每命中一次得2分,没有命中得0分.该射手每次射击的结果相互独立.假设该射手完成以上三次射击. (Ⅰ)求该射手恰好命中一次得的概率;
(Ⅱ)求该射手的总得分X的分布列及数学期望EX.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn , 并且满足2Sn=an2+n,an>0(n∈N*).
(1)求a1 , a2 , a3;
(2)猜想{an}的通项公式,并加以证明;
(3)设x>0,y>0,且x+y=1,证明: ![]() ≤
≤ ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com