
【题目】已知函数![]() 若函数
若函数![]() 恰有
恰有![]() 个不同的零点,则实数
个不同的零点,则实数![]() 的取值范围是__________.
的取值范围是__________.
【答案】(3/2,2)
【解析】g(x)=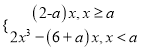 ,
,
显然,当a=2时,g(x)有无穷多个零点,不符合题意;
当x≥a时,令g(x)=0得x=0,
当x<a时,令g(x)=0得x=0或x2=![]() ,
,
(1)若a>0且a≠2,则g(x)在[a,+∞)上无零点,在(﹣∞,a)上存在零点x=0和x=-![]() ,∴
,∴![]() ≥a,解得0<a<2,
≥a,解得0<a<2,
(2)若a=0,则g(x)在[0,+∞)上存在零点x=0,在(﹣∞,0)上存在零点x=﹣![]() ,
,
符合题意;
(3)若a<0,则g(x)在[a,+∞)上存在零点x=0,
∴g(x)在(﹣∞,a)上只有1个零点,∵0(﹣∞,a),∴g(x)在(﹣∞,a)上的零点为x=﹣![]() ,
,
∴﹣![]() <a,解得﹣<a<0.
<a,解得﹣<a<0.
综上,a的取值范围是(![]() ,2).
,2).
故答案为(![]() ,2).
,2).


科目:高中数学 来源: 题型:
【题目】如图,四棱锥PABC中,PA⊥底面ABCD,AD∥BC,AB=AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD,N为PC的中点.

(Ⅰ)证明MN∥平面PAB;
(Ⅱ)求直线AN与平面PMN所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】李明自主创业,在网上经营一家水果店,销售的水果中有草莓、京白梨、西瓜、桃,价格依次为60元/盒、65元/盒、80元/盒、90元/盒.为增加销量,李明对这四种水果进行促销:一次购买水果的总价达到120元,顾客就少付x元.每笔订单顾客网上支付成功后,李明会得到支付款的80%.
①当x=10时,顾客一次购买草莓和西瓜各1盒,需要支付__________元;
②在促销活动中,为保证李明每笔订单得到的金额均不低于促销前总价的七折,则x的最大值为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小明跟父母、爷爷奶奶一同参加《中国诗词大会》的现场录制,5人坐成一排.若小明的父母至少有一人与他相邻,则不同坐法的总数为
A. 60 B. 72 C. 84 D. 96
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动圆过定点![]() ,且在
,且在![]() 轴上截得弦
轴上截得弦![]() 的长为4。
的长为4。
(1)求动圆圆心的轨迹![]() 的方程;
的方程;
(2)设![]() ,过点
,过点![]() 斜率为
斜率为![]() 的直线
的直线![]() 交轨迹
交轨迹![]() 于
于![]() 两点,
两点, ![]() 的延长线交轨迹
的延长线交轨迹![]() 于
于![]() 两点。
两点。
①若![]() 的面积为3,求
的面积为3,求![]() 的值。
的值。
②记直线![]() 的斜率为
的斜率为![]() ,证明:
,证明: ![]() 为定值,并求出这个定值。
为定值,并求出这个定值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 过点
过点![]() ,直线
,直线![]() 过点
过点![]() 与抛物线
与抛物线![]() 交于
交于![]() ,
, ![]() 两点.点
两点.点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,连接
,连接![]() .
.

(1)求抛物线线![]() 的标准方程;
的标准方程;
(2)问直线![]() 是否过定点?若是,求出定点坐标;若不是,请说明理由.
是否过定点?若是,求出定点坐标;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了贯彻落实中央省市关于新型冠状病毒肺炎疫情防控工作要求,积极应对新型冠状病毒疫情,切实做好2020年春季开学工作,保障校园安全稳定,普及防控知识,确保师生生命安全和身体健康.某校开学前,组织高三年级800名学生参加了“疫情防控”网络知识竞赛(满分150分).已知这800名学生的成绩均不低于90分,将这800名学生的成绩分组如下:第一组![]() ,第二组
,第二组![]() ,第三组
,第三组![]() ,第四组
,第四组![]() ,第五组
,第五组![]() ,第六组
,第六组![]() ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.

(1)求![]() 的值并估计这800名学生的平均成绩(同一组中的数据用该组区间的中点值代表);
的值并估计这800名学生的平均成绩(同一组中的数据用该组区间的中点值代表);
(2)该校“群防群控”督查组为更好地督促高三学生的“个人防控”,准备从这800名学生中取2名学生参与督查工作,其取办法是:先在第二组第五组第六组中用分层抽样的方法抽取6名学生,再从这6名学生中随机抽取2名学生.记这2名学生的竞赛成绩分别为![]()
![]() .求事件
.求事件![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系中,已知圆![]() 的圆心坐标为
的圆心坐标为![]() ,半径为
,半径为![]() ,以坐标原点为极点,
,以坐标原点为极点, ![]() 轴正半轴为极轴,建立极坐标系,直线
轴正半轴为极轴,建立极坐标系,直线![]() 的参数方程为:
的参数方程为: ![]() (
(![]() 为参数)
为参数)
(1)求圆![]() 和直线
和直线![]() 的极坐标方程;
的极坐标方程;
(2)点![]() 的极坐标为
的极坐标为![]() ,直线
,直线![]() 与圆
与圆![]() 相较于
相较于![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com