
【题目】如图,已知矩形![]() 所在平面垂直于直角梯形
所在平面垂直于直角梯形![]() 所在平面于直线
所在平面于直线![]() ,且
,且![]() ,
, ![]() 且
且![]() ∥
∥![]() .
.
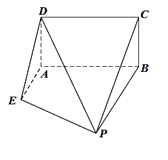
(Ⅰ)设点![]() 为棱
为棱![]() 中点,求证:
中点,求证: ![]() 平面
平面![]() ;
;
(Ⅱ)线段![]() 上是否存在一点
上是否存在一点![]() ,使得直线
,使得直线![]() 与平面
与平面![]() 所成角的正弦值等于
所成角的正弦值等于![]() ?若存在,试确定点
?若存在,试确定点![]() 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
【答案】(Ⅰ)证明见解析;(Ⅱ)当点![]() 与点
与点![]() 重合时,直线
重合时,直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,理由见解析.
,理由见解析.
【解析】试题分析:(1)由平面![]() 平面
平面![]() ,及
,及![]() 为矩形可知
为矩形可知![]() ,所以
,所以![]() 平面
平面![]() ,可以
,可以![]() 为原点,
为原点,![]() 为坐标轴建立空间直角坐标系,从而利用向量得到
为坐标轴建立空间直角坐标系,从而利用向量得到![]() ,平面
,平面![]() 的方向向量
的方向向量![]() ,通过
,通过![]() 证明
证明![]() 平面
平面![]() ;(2)可求得平面
;(2)可求得平面![]() 的方向向量
的方向向量![]() ,
, ![]() 与平面
与平面![]() 的夹角和
的夹角和![]() 与
与![]() 的夹角互余,通过向量的运算即可求得
的夹角互余,通过向量的运算即可求得![]() 坐标.
坐标.
试题解析:(1)证明:由已知,平面![]() 平面
平面![]() ,且
,且![]() ,则
,则![]() 平面
平面![]() ,所以
,所以![]() 两两垂直,故以
两两垂直,故以![]() 为原点,
为原点, ![]() 分别为
分别为![]() 轴
轴![]() 轴,
轴, ![]() 轴正方向,建立如图所示的空间直角坐标系 .
轴正方向,建立如图所示的空间直角坐标系 .
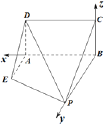
则![]() ,所以
,所以![]() .
.
易知平面![]() 的一个法向量等于
的一个法向量等于![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
又![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
(2)当点![]() 与点
与点![]() 重合时,直线
重合时,直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.
理由如下:
因为![]() ,设平面
,设平面![]() 的法向量为
的法向量为![]() ,
,
由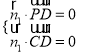 ,得
,得![]() ,
,
即![]() ,得平面
,得平面![]() 的一个法向量等于
的一个法向量等于![]() ,
,
假设线段![]() 上存在一点
上存在一点![]() ,使得直线
,使得直线![]() 与平面
与平面![]() 所成的角
所成的角![]() 的正弦值等于
的正弦值等于![]() .
.
设![]() ,
,
则![]() .
.
所以
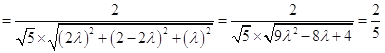 .
.
所以![]() ,解得
,解得![]() 或
或![]() (舍去)
(舍去)
因此,线段![]() 上存在一点
上存在一点![]() ,当
,当![]() 点与
点与![]() 点重合时,直线
点重合时,直线![]() 与平面
与平面![]() 所成角的正弦值等于
所成角的正弦值等于![]() .
.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:高中数学 来源: 题型:
【题目】如下图,已知点![]() 是离心率为
是离心率为![]() 的椭圆
的椭圆![]() :
: ![]() 上的一点,斜率为
上的一点,斜率为![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() 、
、![]() 两点,且
两点,且![]() 、
、![]() 、
、![]() 三点互不重合.
三点互不重合.

(1)求椭圆![]() 的方程;
的方程;
(2)求证:直线![]() ,
, ![]() 的斜率之和为定值.
的斜率之和为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x(1-![]() )是R上的偶函数.
)是R上的偶函数.
(1)对任意的x∈[1,2],不等式m·![]() ≥2x+1恒成立,求实数m的取值范围.
≥2x+1恒成立,求实数m的取值范围.
(2)令g(x)=1-![]() ,设函数F(x)=g(4x-n)-g(2x+1-3)有零点,求实数n的取值范围.
,设函数F(x)=g(4x-n)-g(2x+1-3)有零点,求实数n的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在梯形ABCD中,AD∥BC,AD⊥DC,BC=2AD,四边形ABEF是矩形,将矩形ABEF沿AB折起到四边形ABE1F1的位置,使平面ABE1F1⊥平面ABCD,M为AF1的中点,如图2.
(1)求证:BE1⊥DC;
(2)求证:DM∥平面BCE1;
(3)判断直线CD与ME1的位置关系,并说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,正方体ABCD-A′B′C′D′的棱长为1,E,F分别是棱AA′,CC′的中点,过直线EF的平面分别与棱BB′、DD′分别交于M,N两点,设BM=x,x∈[0,1],给出以下四个结论:

①平面MENF⊥平面BDD′B′;
②直线AC∥平面MENF始终成立;
③四边形MENF周长L=f(x),x∈[0,1]是单调函数;
④四棱锥C′-MENF的体积V=h(x)为常数;
以上结论正确的是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校从参加安全知识竞赛的同学中,选取60名同学将其成绩(百分制,均为整数,成绩![]() 分记为优秀)分成6组后,得到部分频率分布直方图(如图),观察图形中的信息,回答下列问题:
分记为优秀)分成6组后,得到部分频率分布直方图(如图),观察图形中的信息,回答下列问题:
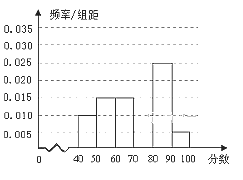
(1)求分数在[70,80)内的频率,并补全这个频率分布直方图;
(2)从频率分布直方图中,估计本次考试的平均分;
(3)为参加市里举办的安全知识竞赛,学校举办预选赛.已知在学校安全知识竞赛中优秀的同学通过预选赛的概率为![]() ,现在从学校安全知识竞赛中优秀的同学中选3人参加预选赛,若随机变量
,现在从学校安全知识竞赛中优秀的同学中选3人参加预选赛,若随机变量![]() 表示这3人中通过预选赛的人数,求
表示这3人中通过预选赛的人数,求![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,以坐标原点
中,以坐标原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴,建立极坐标系,已知直线
轴的正半轴为极轴,建立极坐标系,已知直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),曲线
为参数),曲线![]() 的极坐标方程是
的极坐标方程是![]() .
.
(1)写出直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,点
两点,点![]() 为
为![]() 的中点,点
的中点,点![]() 的极坐标为
的极坐标为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直三棱柱![]() 中,底面为等腰直角三角形,
中,底面为等腰直角三角形, ![]() ,
, ![]() , 若
, 若![]() 、
、![]() 、
、![]() 别是棱
别是棱![]() 、
、![]() 、
、![]() 的中点,则下列四个命题:
的中点,则下列四个命题:
![]() ;
;
②三棱锥![]() 的外接球的表面积为
的外接球的表面积为![]() ;
;
③三棱锥![]() 的体积为
的体积为![]() ;
;
④直线![]() 与平面
与平面![]() 所成角为
所成角为![]()
其中正确的命题有__________.(把所有正确命题的序号填在答题卡上)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com