分析:(1)取A
1D
1中点E,连接ME、C
1E推知MC∥EC,推知A
1N∥MC且MC=A
1N,得到A
1,M,C,N四点共面.
(2)连接BD,得到BD是D
1B在平面ABCD内的射影,得到
==,得到Rt△CDM~Rt△BCD,得到∠DCM=∠CBD,得到MC⊥BD,从而得到D
1B⊥MC.
(3)连接A
1C,由A
1BCD
1是正方形,得到D
1B⊥A
1C.由D
1B⊥MC,得到D
1B⊥平面A
1MCN,得到平面A
1MCN⊥平面A
1BD
1.
(4)由(2)(3)得到∠BA
1C是A
1B与平面A
1MCN所成的角.
解答: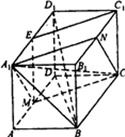
解:(1)取A
1D
1中点E,连接ME、C
1E,
∴A
1N∥C
1E且C
1E=A
1N,MC∥EC、
∴A
1N∥MC且MC=A
1N∴A
1,M,C,N四点共面.
(2)连接BD,则BD是D
1B在平面ABCD内的射影.
∵
==,∴Rt△CDM~Rt△BCD,∠DCM=∠CBD、
∴∠CBD+∠BCM=90°.∴MC⊥BD、∴D
1B⊥MC.
(3)连接A
1C,由A
1BCD
1是正方形,知D
1B⊥A
1C.
∵D
1B⊥MC,∴D
1B⊥平面A
1MCN.
∴平面A
1MCN⊥平面A
1BD
1.
(4)由(3)知平面A
1MCN⊥平面A
1BD
1.
∴A
1C是直线A
1B在平面A
1MCN内的身影
∴∠BA
1C是A
1B与平面A
1MCN所成的角
又∵A
1B⊥BC,A
1B=BC
∴∠BA
1C=45°
点评:本题主要考查平面图形的量的关系来推知空间线线位置关系,进而得到线面,面面位置关系.

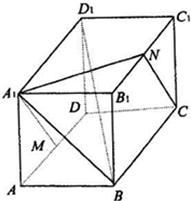 如图,长方体ABCD-A1B1C1D1中,AB=A1A=a,BC=
如图,长方体ABCD-A1B1C1D1中,AB=A1A=a,BC= 解:(1)取A1D1中点E,连接ME、C1E,
解:(1)取A1D1中点E,连接ME、C1E,

 阅读快车系列答案
阅读快车系列答案 19、如图,长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,点P为DD1的中点.
19、如图,长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,点P为DD1的中点. 15、如图,长方体ABCD-A1B1C1D1中被截去一部分,
15、如图,长方体ABCD-A1B1C1D1中被截去一部分, 如图在长方体ABCD-A1B1C1D1中,其中AB=BC,E,F分别是AB1,BC1的中点,则以下结论中
如图在长方体ABCD-A1B1C1D1中,其中AB=BC,E,F分别是AB1,BC1的中点,则以下结论中 如图,长方体ABCD-A1B1C1D1中,P是线段AC的中点.
如图,长方体ABCD-A1B1C1D1中,P是线段AC的中点.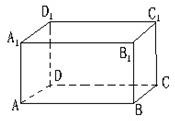 已知如图:长方体ABCD-A1B1C1D1中,交于顶点A的三条棱长别为AD=3,AA1=4,AB=5.一天,小强观察到在A处有一只蚂蚁,发现顶点C1处有食物,于是它沿着长方体的表面爬行去获取食物,则蚂蚁爬行的最短路程是( )
已知如图:长方体ABCD-A1B1C1D1中,交于顶点A的三条棱长别为AD=3,AA1=4,AB=5.一天,小强观察到在A处有一只蚂蚁,发现顶点C1处有食物,于是它沿着长方体的表面爬行去获取食物,则蚂蚁爬行的最短路程是( )