
【题目】已知函数f(x)=x﹣1+ ![]() ,(a∈R,e为自然对数的底数).
,(a∈R,e为自然对数的底数).
(1)求函数f(x)的单调区间;
(2)当a=1时,若直线l:y=kx﹣1与曲线y=f(x)没有公共点,求k的最大值.
【答案】
(1)解:∵f(x)=x﹣1+ ![]() ,
,
∴f′(x)=1﹣ ![]() =
= ![]() ,由f′(x)=0得x=lna
,由f′(x)=0得x=lna
∴当x∈(﹣∞,lna)时,f′(x)<0,∴(﹣∞,lna)是f(x)的单调递减区间;
当x∈(lna,+∞)时,f′(x)>0,∴(lna,+∞)是f(x)的单调递增区间
(2)解:当a=1时,若直线l:y=kx﹣1与曲线y=f(x)=x﹣1+ ![]() 没有公共点,则x﹣1+
没有公共点,则x﹣1+ ![]() =kx﹣1无解,
=kx﹣1无解,
∵x=0时,上述方程不成立,∴x≠0
则x﹣1+ ![]() =kx﹣1可化为k=1+
=kx﹣1可化为k=1+ ![]() ,
,
设g(x)=1+ ![]() ,∴g′(x)=
,∴g′(x)= ![]()
∴g′(x)满足:在(﹣∞,﹣1)上g′(x)>0,在(﹣1,0)上g′(x)<0,在(0,+∞)上g′(x)<0,
∴g(x)满足:在(﹣∞,﹣1)上递增,在(﹣1,0)上递减,在(0,+∞)上递减,
g(﹣1)=1﹣e,而当x→+∞时,g(x)→1,
∴g(x)的图象:
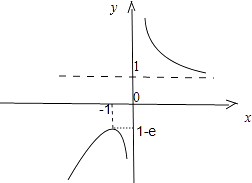
∴g(x)∈(﹣∞,1﹣e]∪(1,+∞)
无解时,k∈(1﹣e,1],
∴kmax=1
【解析】(1)先求导,f′(x)=1﹣ ![]() =
= ![]() ,由f′(x)=0得x=lna,分x∈(﹣∞,lna)与(﹣∞,lna)两种情况写出f(x)的单调递减区间;(2)当a=1时,若直线l:y=kx﹣1与曲线y=f(x)=x﹣1+
,由f′(x)=0得x=lna,分x∈(﹣∞,lna)与(﹣∞,lna)两种情况写出f(x)的单调递减区间;(2)当a=1时,若直线l:y=kx﹣1与曲线y=f(x)=x﹣1+ ![]() 没有公共点,则x﹣1+
没有公共点,则x﹣1+ ![]() =kx﹣1无解,则x﹣1+
=kx﹣1无解,则x﹣1+ ![]() =kx﹣1可化为k=1+
=kx﹣1可化为k=1+ ![]() ,
,
设g(x)=1+ ![]() ,求导,研究此函数的单调性即可解决.
,求导,研究此函数的单调性即可解决.
【考点精析】根据题目的已知条件,利用函数的最值及其几何意义和利用导数研究函数的单调性的相关知识可以得到问题的答案,需要掌握利用二次函数的性质(配方法)求函数的最大(小)值;利用图象求函数的最大(小)值;利用函数单调性的判断函数的最大(小)值;一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减.
在这个区间单调递减.


 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案科目:高中数学 来源: 题型:
【题目】某工厂为了对新研发的一种产品进行合理定价,将该产品按事先拟订的价格进行试销得到如下数据:
单价x(元) | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
销量y(件) | 92 | 82 | 83 | 80 | 75 | 68 |
(1)求出y关于x的线性回归方程 ![]() .其中
.其中 ![]() =250
=250
(2)预计在今后的销售中,销量与单价仍然服从(I)中的关系,且该产品的成本是4元每件,为使工厂获得最大利润,该产品的单价应定为多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在对人们休闲方式的一次调查中,共调查120人,其中女性70人、男性50人,女性中有40人主要的休闲方式是看电视,另外30人主要的休闲方式是运动;男性中有20人主要的休闲方式是看电视,另外30人主要的休闲方式是运动.
(1)根据以上数据建立一个2×2的列联表;
(2)在犯错误的概率不超过0.10的前提下,认为休闲方式与性别是否有关?
参考数据:独立性检验临界值表
p(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
K2= ![]() ,n=a+b+c+d.
,n=a+b+c+d.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=f(x)满足f(x﹣1)=2x+3a,且f(a)=7.
(1)求函数f(x)的解析式;
(2)若g(x)=xf(x)+λf(x)+x在[0,2]上最大值为2,求实数λ的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某次水下科研考察活动中,需要潜水员潜入水深为60米的水底进行作业,根据以往经验,潜水员下潜的平均速度为![]() (米/单位时间),每单位时间的用氧量为
(米/单位时间),每单位时间的用氧量为![]() (升),在水底作业10个单位时间,每单位时间用氧量为0.9(升),返回水面的平均速度为
(升),在水底作业10个单位时间,每单位时间用氧量为0.9(升),返回水面的平均速度为![]() (米/单位时间),每单位时间用氧量为1.5(升),记该潜水员在此次考察活动中的总用氧量为
(米/单位时间),每单位时间用氧量为1.5(升),记该潜水员在此次考察活动中的总用氧量为![]() (升).
(升).
(1)求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)若![]() ,求当下潜速度
,求当下潜速度![]() 取什么值时,总用氧量最少.
取什么值时,总用氧量最少.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某产品生产厂家根据以往的生产销售经验得到下面有关生产销售的统计规律:每生产产品x(百台),其总成本为G(x)(万元),其中固定成本为2.8万元,并且每生产1百台的生产成本为1万元(总成本=固定成本+生产成本).销售收入R(x)(万元)满足 ![]() ,假定该产品产销平衡(即生产的产品都能卖掉),根据上述统计规律,请完成下列问题:
,假定该产品产销平衡(即生产的产品都能卖掉),根据上述统计规律,请完成下列问题:
(1)写出利润函数y=f(x)的解析式(利润=销售收入﹣总成本);
(2)要使工厂有盈利,求产量x的范围;
(3)工厂生产多少台产品时,可使盈利最多?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com