
分析 先求出抛物线的方程,再求出抛物线在点B处的切线方程,即可求△BFC的面积.
解答 解:由题意F($\frac{p}{2}$,0),B($\frac{p}{4}$,$\sqrt{2}$),
∵B在抛物线上,
∴2=$\frac{{p}^{2}}{2}$,
∵p>0,
∴p=2,
∴抛物线y2=4x,B($\frac{1}{2}$,$\sqrt{2}$),
由y=2$\sqrt{x}$,可得y′=$\frac{1}{\sqrt{x}}$,x=$\frac{1}{2}$时,y′=$\sqrt{2}$,
∴抛物线在点B处的切线方程为y-$\sqrt{2}$=$\sqrt{2}$(x-$\frac{1}{2}$),
y=0时,x=-$\frac{1}{2}$,∴△BFC的面积为$\frac{1}{2}×(1+\frac{1}{2})×\sqrt{2}$=$\frac{3\sqrt{2}}{4}$.
故答案为:$\frac{3\sqrt{2}}{4}$.
点评 本题考查抛物线的方程,考查导数的几何意义,考查学生的计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | (x-4)2+(y+1)2=1 | B. | (x+4)2+(y+1)2=1 | C. | (x+2)2+(y+4)2=1 | D. | (x-2)2+(y+1)2=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 周一 | 无雨 | 无雨 | 有雨 | 有雨 |
| 周二 | 无雨 | 有雨 | 无雨 | 有雨 |
| 收益 | 20万 | 15万 | 10万 | 7.5万 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
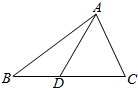 如图,在△ABC中,AB=12,$AC=3\sqrt{6}$,$BC=5\sqrt{6}$,点D在边BC上,且∠ADC=60°.
如图,在△ABC中,AB=12,$AC=3\sqrt{6}$,$BC=5\sqrt{6}$,点D在边BC上,且∠ADC=60°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com