
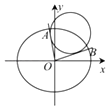
【题目】如图所示,已知椭圆C: ![]() +
+ ![]() =1(a>b>0)的焦距为2,直线y=x被椭圆C截得的弦长为
=1(a>b>0)的焦距为2,直线y=x被椭圆C截得的弦长为 ![]() .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)设点M(x0 , y0)是椭圆C上的动点,过原点O引两条射线l1 , l2与圆M:(x﹣x0)2+(y﹣y0)2= ![]() 分别相切,且l1 , l2的斜率k1 , k2存在.
分别相切,且l1 , l2的斜率k1 , k2存在.
①试问k1k2是否定值?若是,求出该定值,若不是,说明理由;
②若射线l1 , l2与椭圆C分别交于点A,B,求|OA||OB|的最大值.
【答案】解:(Ⅰ)由2c=2,c=1,设直线直线y=x被与椭圆C相交于P,Q两点,
则丨OP丨= ![]() ,设P(
,设P( ![]() ,
, ![]() ),代入椭圆方程,
),代入椭圆方程, ![]() ,①
,①
由a2﹣b2=1,②
解得:a2=2,b2=1,
∴椭圆的标准方程: ![]() ;
;
(Ⅱ)①设射线l的方程y=kx,A(x1 , y1),B(x2 , y2),
由 ![]() =
= ![]() ,两边平方得(3x02﹣2)k2﹣6x0y0k+3y02﹣2=0,
,两边平方得(3x02﹣2)k2﹣6x0y0k+3y02﹣2=0,
由y02=1﹣ ![]() ,
,
∴k1k2= ![]() =
= 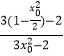 =﹣
=﹣ ![]() ,
,
∴k1k2为定值,定值﹣ ![]() ,
,
②方法一:联立 ![]() ,消去y,x12=
,消去y,x12= ![]() ,丨OA丨=
,丨OA丨= ![]() ,同理丨OA丨=
,同理丨OA丨= ![]() ,
,
|OA|2|OB|2= ![]()
![]() =4×
=4× ![]() =
= ![]() =2+
=2+ ![]() ,
,
=2+ 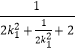 ≤
≤ ![]() ,当且仅当k12=
,当且仅当k12= ![]() ,取等号,
,取等号,
∴|OA||OB|的最大值为 ![]() ,
,
方法二:联立 ![]() ,消去y,x12=
,消去y,x12= ![]() ,丨OA丨=
,丨OA丨= ![]() ,同理丨OA丨=
,同理丨OA丨= ![]() ,
,
则|OA|2+|OB|2= ![]() +
+ ![]() =
= ![]() +
+ ![]() =
= ![]() +
+ ![]() =3,
=3,
由|OA|2+|OB|2≥2|OA||OB|,则|OA||OB|≤ ![]() ,当且仅当|OA|=|OB|时,取等号,
,当且仅当|OA|=|OB|时,取等号,
∴|OA||OB|的最大值 ![]() .
.
【解析】(Ⅰ)由c=2,求得P点坐标,代入椭圆方程,由a2﹣b2=1,即可求得a和b的值,即可求得椭圆方程;(Ⅱ)①设射线l的方程y=kx,代入椭圆方程,由韦达定理即可求得k1k2= ![]() ,由y02=1﹣
,由y02=1﹣ ![]() ,即可求得k1k2=﹣
,即可求得k1k2=﹣ ![]() ;②方法一:分别求得直线OA及OB的方程代入椭圆方程,求得|OA|及|OB|,利用基本不等式的性质,即可求得|OA||OB|的最大值;
;②方法一:分别求得直线OA及OB的方程代入椭圆方程,求得|OA|及|OB|,利用基本不等式的性质,即可求得|OA||OB|的最大值;
方法二:|OA|2+|OB|2= ![]() +
+ ![]() ,y02=1﹣
,y02=1﹣ ![]() ,代入即可求得:|OA|2+|OB|2=3,由|OA|2+|OB|2≥2|OA||OB|,即可求得|OA||OB|的最大值.
,代入即可求得:|OA|2+|OB|2=3,由|OA|2+|OB|2≥2|OA||OB|,即可求得|OA||OB|的最大值.
【考点精析】解答此题的关键在于理解椭圆的标准方程的相关知识,掌握椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】设△ABC的内角A、B、C的对边分别为a、b、c,且满足sinA+sinB=[cosA﹣cos(π﹣B)]sinC.
(1)试判断△ABC的形状,并说明理由;
(2)若a+b+c=1+ ![]() ,试求△ABC面积的最大值.
,试求△ABC面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某班举行的“庆五一”联欢晚会开幕前已排好有8个不同节目的节目单,如果保持原来的节目相对顺序不变,临时再插进去![]() 三个不同的新节目,且插进的三个新节目按
三个不同的新节目,且插进的三个新节目按![]() 顺序出场,那么共有__________种不同的插入方法(用数字作答).
顺序出场,那么共有__________种不同的插入方法(用数字作答).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶4元,售价每瓶6元,未售出的酸奶降价处理,以每瓶2元的价格当天全部处理完.根据往年销售经验,每天需求量与当天最高气温(单位:![]() )有关.如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间
)有关.如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间![]() ,需求量为300瓶;如果最高气温低于20,需求量为200瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:
,需求量为300瓶;如果最高气温低于20,需求量为200瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:
![]()
以最高气温位于各区间的频率估计最高气温位于该区间的概率.
(1)求六月份这种酸奶一天的需求量![]() (单位:瓶)的分布列;
(单位:瓶)的分布列;
(2)设六月份一天销售这种酸奶的利润为![]() (单位:元),当六月份这种酸奶一天的进货量
(单位:元),当六月份这种酸奶一天的进货量![]() (单位:瓶)为多少时,
(单位:瓶)为多少时,![]() 的数学期望达到最大值?
的数学期望达到最大值?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x3+ax2+bx+c,x∈[-2,2]表示过原点的曲线,且在x=±1处的切线的倾斜角均为![]() π,有以下命题:
π,有以下命题:
①f(x)的解析式为f(x)=x3-4x,x∈[-2,2].
②f(x)的极值点有且只有一个.
③f(x)的最大值与最小值之和等于零.
其中正确命题的序号为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设集合A={x|x2-3x+2=0},B={x|x2+(a-1)x+a2-5=0}.
(1)若A∩B={2},求实数a的值;
(2)若A∪B=A,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分) 某校为了解高一期末数学考试的情况,从高一的所有学生数学试卷中随机抽取![]() 份试卷进行成绩分析,得到数学成绩频率分布直方图(如图所示),其中成绩在
份试卷进行成绩分析,得到数学成绩频率分布直方图(如图所示),其中成绩在![]() ,
,![]() 的学生人数为6.
的学生人数为6.
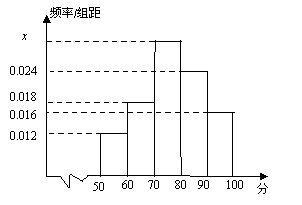
(Ⅰ)求直方图中![]() 的值;
的值;
(Ⅱ)试估计所抽取的数学成绩的平均数;
(Ⅲ)试根据样本估计“该校高一学生期末数学考试成绩![]() ”的概率.
”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A、F分别是椭圆C: ![]() +
+ ![]() =1(a>b>0)的左顶点、右焦点,点P为椭圆C上一动点,当PF⊥x轴时,AF=2PF.
=1(a>b>0)的左顶点、右焦点,点P为椭圆C上一动点,当PF⊥x轴时,AF=2PF.
(1)求椭圆C的离心率;
(2)若椭圆C存在点Q,使得四边形AOPQ是平行四边形(点P在第一象限),求直线AP与OQ的斜率之积;
(3)记圆O:x2+y2= ![]() 为椭圆C的“关联圆”.若b=
为椭圆C的“关联圆”.若b= ![]() ,过点P作椭圆C的“关联圆”的两条切线,切点为M、N,直线MN的横、纵截距分别为m、n,求证:
,过点P作椭圆C的“关联圆”的两条切线,切点为M、N,直线MN的横、纵截距分别为m、n,求证: ![]() +
+ ![]() 为定值.
为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com