已知集合A={x|x2-2x-8≤0,x∈R},B={x|x2-(2m-3)x+m2-3m≤0,x∈R,m∈R }.
(1)若A∩B=[2,4],求实数m的值;
(2)设全集为R,若A⊆?RB,求实数m的取值范围.
解:(1)由已知得A={x|x
2-2x-8≤0,x∈R}=[-2,4],
B={x|x
2-(2m-3)x+m
2-3m≤0,x∈R,m∈R }=[m-3,m].
∵A∩B=[2,4],∴
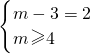
∴m=5.
(2)∵B=[m-3,m],∴?
RB=(-∞,m-3)∪(m,+∞).
∵A⊆?
RB,
∴m-3>4或m<-2.
∴m>7或m<-2.
∴m∈(-∞,-2)∪(7,+∞).
分析:(1)根据所给的两个集合的不等式,写出两个集合对应的最简形式,根据两个集合的交集,看出两个集合的端点之间的关系,求出结果.
(2)根据所求的集合B,写出集合B的补集,根据集合A是B的补集的子集,求出两个集合的端点之间的关系,求出m的值.
点评:本题考查集合之间的关系与参数的取值,本题解题的关键是利用集合之间的关系,得到不等式之间的关系,本题是一个基础题.

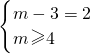 ∴m=5.
∴m=5.

 习题精选系列答案
习题精选系列答案