
【题目】如图,在四棱锥![]() 中,
中,![]() ,
,![]() ,
,![]() ,且PC=BC=2AD=2CD=2
,且PC=BC=2AD=2CD=2![]() ,
,![]() .
.
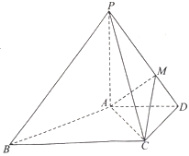
(1)![]() 平面
平面![]() ;
;
(2)已知点![]() 在线段
在线段![]() 上,且
上,且![]() ,求点
,求点![]() 到平面
到平面![]() 的距离.
的距离.
【答案】(1)见证明;(2)![]()
【解析】
(1)要证![]() 平面
平面![]() ,只需证明
,只需证明![]() ,
,![]() 即可.由勾股定理易证
即可.由勾股定理易证![]() ,又由
,又由![]() 可得
可得 ![]() 平面
平面![]() ,进而可得
,进而可得![]() ,因此可得结论成立.
,因此可得结论成立.
(2)法一:可由等体积法求解,由![]() ,易得点
,易得点![]() 到平面
到平面![]() 的距离;
的距离;
法二:先证![]() ,由三角形相似,也可求出点
,由三角形相似,也可求出点![]() 到平面
到平面![]() 的距离.
的距离.
(1)∵在底面![]() 中,
中,![]() ,
,![]()
且![]()
∴![]() ,
,![]() ∴
∴![]()
又∵![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]()
∴![]() 平面
平面![]() 又∵
又∵![]() 平面
平面![]() ∴
∴![]()
∵![]() ,
,![]() ∴
∴![]()
又∵![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]()
∴![]() 平面
平面![]()
(2)方法一:在线段![]() 上取点
上取点![]() ,使
,使![]() ,则
,则![]()
又由(1)得![]() 平面
平面![]() ,
,![]() 平面
平面![]()
又∵![]() 平面
平面![]() ,∴
,∴![]()
作![]() 于
于![]() 又∵
又∵![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]()
∴![]() 平面
平面![]() 又∵
又∵![]() 平面
平面![]() ∴
∴![]()
设点![]() 到平面
到平面![]() 的距离为
的距离为![]()
则由![]() 得
得![]()
∴点![]() 到平面
到平面![]() 的距离
的距离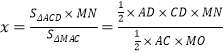
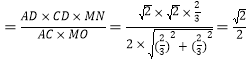
方法二:由(1)知![]() 平面
平面![]() ,∴平面
,∴平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]()
∵![]() ,平面
,平面![]() 平面
平面![]() ∴
∴![]() 平面
平面![]()
∴平面![]() 平面
平面![]() ①
①
又∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ∴
∴![]()
![]() ,
,![]() ,∴
,∴![]() ,∴
,∴![]()
∴![]() ∴
∴![]() ∴
∴![]() ②
②
平面![]() 平面
平面![]() ③
③
由①②③得![]() 平面
平面![]() ,∴平面
,∴平面![]() 平面
平面![]()
又∵平面![]() 平面
平面![]() ∴过
∴过![]() 作
作![]() 交
交![]() 于点
于点![]() ∴
∴![]() 平面
平面![]()
即![]() 的长就是点
的长就是点![]() 到平面
到平面![]() 的距离.
的距离.
在![]() 中,
中,![]() ,
,![]()
∴![]()


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】[2019·清远期末]一只红铃虫的产卵数![]() 和温度
和温度![]() 有关,现收集了4组观测数据列于下表中,根据数据作出散点图如下:
有关,现收集了4组观测数据列于下表中,根据数据作出散点图如下:
温度 | 20 | 25 | 30 | 35 |
产卵数 | 5 | 20 | 100 | 325 |

(1)根据散点图判断![]() 与
与![]() 哪一个更适宜作为产卵数
哪一个更适宜作为产卵数![]() 关于温度
关于温度![]() 的回归方程类型?(给出判断即可,不必说明理由)
的回归方程类型?(给出判断即可,不必说明理由)
(2)根据(1)的判断结果及表中数据,建立![]() 关于
关于![]() 的回归方程(数字保留2位小数);
的回归方程(数字保留2位小数);
(3)要使得产卵数不超过50,则温度控制在多少![]() 以下?(最后结果保留到整数)
以下?(最后结果保留到整数)
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
| 5 | 20 | 100 | 325 |
| 1.61 | 3 | 4.61 | 5.78 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,圆C:![]()
(1)若圆C与x轴相切,求实数a的值;
(2)若M,N为圆C上不同的两点,过点M,N分别作圆C的切线![]() ,若
,若![]() 与
与![]() 相交于点P,圆C上异于M,N另有一点Q,满足
相交于点P,圆C上异于M,N另有一点Q,满足![]() ,若直线
,若直线![]() :
:![]() 上存在唯一的一个点T,使得
上存在唯一的一个点T,使得![]() ,求实数a的值.
,求实数a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中,![]() ,
,![]() ,
,![]() ,且
,且![]() ,
,![]() .
.
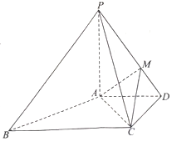
(1)证明:![]() 平面
平面![]() ;
;
(2)在线段![]() 上,是否存在一点
上,是否存在一点![]() ,使得二面角
,使得二面角![]() 的大小为
的大小为![]() ?如果存在,求
?如果存在,求![]() 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=Asin(ωx+φ) ![]() 的部分图象如图所示.
的部分图象如图所示.

(1)求函数y=f(x)的解析式;
(2)求f(x)的单调减区间
(3)当![]() 时,求f(x)的取值范围.
时,求f(x)的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从甲地到乙地要经过3个十字路口,设各路口信号灯工作相互独立,且在各路口遇到红灯的概率分别为![]() .
.
(Ⅰ)设![]() 表示一辆车从甲地到乙地遇到红灯的个数,求随机变量
表示一辆车从甲地到乙地遇到红灯的个数,求随机变量![]() 的分布列和数学期望;
的分布列和数学期望;
(Ⅱ)若有2辆车独立地从甲地到乙地,求这2辆车共遇到1个红灯的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 和椭圆
和椭圆![]() . 直线
. 直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() .
.
(Ⅰ) 求椭圆![]() 的离心率;
的离心率;
(Ⅱ) 当![]() 时,求
时,求![]() 的面积;
的面积;
(Ⅲ)设直线![]() 与椭圆
与椭圆![]() 的另一个交点为
的另一个交点为![]() ,当
,当![]() 为
为![]() 中点时,求
中点时,求![]() 的值 .
的值 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com