
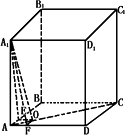
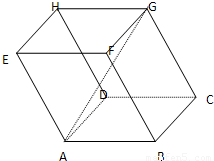
如图,平行六面体ABCD-A1B1C1D1的底面是边长为1的正方形,侧棱AA1长为2,且∠A1AB=∠A1AD=60°则此平行六面体的体积为________
|
解法一:过点A1做A1O⊥平面ABCD,垂足为O,过O做OE⊥AB,OF⊥AD,垂足分别为E、F,连结A1E,A1F,可知O在∠BAD的平分线AC上. ∴cos∠A1AO·cos∠OAF= 即cos∠A1AO·cos45°=cos60° ∴cos∠A1AO= ∴sin∠A1AO= ∴A1O=A1Asin∠A1AO= ∴V=SABCD·A1O= 解法二:过B作BE⊥A1A,连结DE,可知面BDE是其直截面,把斜三棱柱分割成上下两部分,若把两部分重新组合,让面A1D1B1与面ADB重合,则得到一直棱柱,ΔBDE是其底面,DD1是其侧棱,并且和斜三棱柱A1B1D1-ABD的体积相等. 取BD中点O,连结OE,易知 SΔBED= = ∴V直棱柱=SΔDEB·DD1 = ∴ 解析一:求平行六面体ABCD-A1B1C1D的体积,应用公式.由于底面是正方形,所以关键是求高,即 分析二:如图,平行六面体的对角面B1D1DB把平行六面体分割成两个斜三棱柱,它们等底面积、等高、体积相等,考察其中之一三棱柱A1B1D1-ABD.
点评:在解决体积问题时,“割”“补”是常用的手段,另外本题分析二给出了求斜棱柱体积的另一方法:斜棱柱的体积=直截面面积×侧棱长. |


 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:高中数学 来源: 题型:
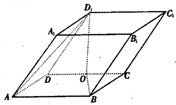 如图,平行六面体ABCD-A1B1C1D1中,AB=2,AD=1,底面ABCD是矩形,顶点D1在底面ABCD上的射影O恰好是CD的中点.
如图,平行六面体ABCD-A1B1C1D1中,AB=2,AD=1,底面ABCD是矩形,顶点D1在底面ABCD上的射影O恰好是CD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:
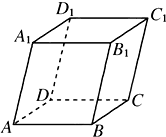 如图,平行六面体ABCD-A1B1C1D1中,∠BAD=∠BAA1=∠DAA1=60°,
如图,平行六面体ABCD-A1B1C1D1中,∠BAD=∠BAA1=∠DAA1=60°,查看答案和解析>>
科目:高中数学 来源:2013届湖北省武汉市高二下期末理科数学试卷(解析版) 题型:解答题
题满分12分)
.如图,平行六面体ABCD-A1B1C1D1中,∠BAD=∠BAA1=∠DAA1=60°,
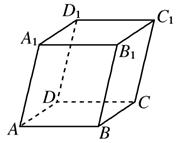
(1)当AA1=3,AB=2,AD=2,求AC1的长;
(2)当底面ABCD是菱形时,求证: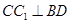
查看答案和解析>>
科目:高中数学 来源:2010-2011学年浙江省杭州市萧山区三校联考高二(上)期中数学试卷(理科)(解析版) 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com