四个不同的小球全部放入编号为1、2、3、4的四个盒中.恰有两个空盒的放法有 种;甲球只能放入2号或3号盒,而乙球不能放入4号盒的不同放法有 种.
【答案】
分析:本题需要先分类,把四个小球先分成两组,每组两个小球,或者是把四个小球分成两组,每组一个和三个,分完小组后再进行排列,从4个盒中选两个位置排列,得到结果.甲球只能放入2号或3号盒,而乙球不能放入4号盒,则甲有2种选法,乙也有3种选法,剩下的两个人在各有4种结果,相乘得到结果.
解答:解:由题意知本题需要先分类,
把四个小球先分成两组,每组两个小球,共有
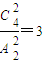
把分成两组的球,在4个何种选两个排列,共有3A
42=36种结果,
把四个小球分成两组,每组一个或三个,再在四个位置选两个位置排列,共有C
43A
42=48种结果,
根据分类计数原理得到共有36+48=84种结果;
甲球只能放入2号或3号盒,而乙球不能放入4号盒,
则甲有2种选法,乙有3种选法,剩下的两个球在两个各有4种结果,
根据分步计数原理知共有2×3×4×4=96种结果,
故答案为:84;96
点评:本题是排列和组合的实际问题的运算,根据题意写出排列组合数,通过加减乘运算,得到结果,这类问题有一大部分是考查排列和组合的区别的,本题是一个基础题.

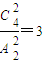


 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案