
【题目】已知点P在直线l:y=x-1上,若存在过点P的直线交抛物线![]() 于A,B两点,且|PA|=|AB|,则称点P为“正点”,那么下列结论中正确的是( )
于A,B两点,且|PA|=|AB|,则称点P为“正点”,那么下列结论中正确的是( )
A.直线l上的所有点都是“正点”
B.直线l上仅有有限个点是“正点”
C.直线l上的所有点都不是“正点”
D.直线l上有无穷多个点(但不是所有的点)是“正点”
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案科目:高中数学 来源: 题型:
【题目】某书店刚刚上市了《中国古代数学史》,销售前该书店拟定了5种单价进行试销,每种单价(![]() 元)试销l天,得到如表单价
元)试销l天,得到如表单价![]() (元)与销量
(元)与销量![]() (册)数据:
(册)数据:
单价 | 18 | 19 | 20 | 21 | 22 |
销量 | 61 | 56 | 50 | 48 | 45 |
(l)根据表中数据,请建立![]() 关于
关于![]() 的回归直线方程:
的回归直线方程:
(2)预计今后的销售中,销量![]() (册)与单价
(册)与单价![]() (元)服从(l)中的回归方程,已知每册书的成本是12元,书店为了获得最大利润,该册书的单价应定为多少元?
(元)服从(l)中的回归方程,已知每册书的成本是12元,书店为了获得最大利润,该册书的单价应定为多少元?
附: ,
,![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】空气质量指数![]() 是检测空气质量的重要参数,其数值越大说明空气污染状况越严重,空气质量越差.某地环保部门统计了该地区某月1日至24日连续24天的空气质量指数
是检测空气质量的重要参数,其数值越大说明空气污染状况越严重,空气质量越差.某地环保部门统计了该地区某月1日至24日连续24天的空气质量指数![]() ,根据得到的数据绘制出如图所示的折线图,则下列说法错误的是( )
,根据得到的数据绘制出如图所示的折线图,则下列说法错误的是( )
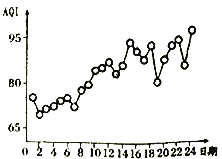
A. 该地区在该月2日空气质量最好
B. 该地区在该月24日空气质量最差
C. 该地区从该月7日到12日![]() 持续增大
持续增大
D. 该地区的空气质量指数![]() 与这段日期成负相关
与这段日期成负相关
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为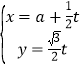 (
(![]() 为参数,
为参数,![]() )以坐标原点
)以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 与
与![]() 有且只有一个公共点.
有且只有一个公共点.
(1)求实数![]() 的值;
的值;
(2)已知点![]() 的直角坐标为
的直角坐标为![]() ,若曲线
,若曲线![]() 与
与![]() :
:![]() (
(![]() 为参数)相交于
为参数)相交于![]() ,
,![]() 两个不同点,求
两个不同点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,以坐标原点
中,以坐标原点![]() 为极点,
为极点,![]() 轴非负半轴为极轴建立极坐标系.已知曲线
轴非负半轴为极轴建立极坐标系.已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 的参数方程为
的参数方程为![]() (
(![]() ,
,![]() 为参数)
为参数)
(1)求曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设直线![]() 与曲线
与曲线![]() 交于
交于![]() 、
、![]() 两点,点
两点,点![]() 的直角坐标为
的直角坐标为![]() ,若
,若![]() ,求直线
,求直线![]() 的普通方程.
的普通方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某次高中学科竞赛中,4000名考生的参赛成绩统计如图所示,60分以下视为不及格,若同一组中数据用该组区间中点作代表,则下列说法中有误的是( )

A. 成绩在![]() 分的考生人数最多
分的考生人数最多
B. 不及格的考生人数为1000人
C. 考生竞赛成绩的平均分约70.5分
D. 考生竞赛成绩的中位数为75分
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正三棱锥![]() 中,侧棱长为3,底面边长为2,E,F分别为棱AB,CD的中点,则下列命题正确的是( )
中,侧棱长为3,底面边长为2,E,F分别为棱AB,CD的中点,则下列命题正确的是( )
A.EF与AD所成角的正切值为![]() B.EF与AD所成角的正切值为
B.EF与AD所成角的正切值为![]()
C.AB与面ACD所成角的余弦值为![]() D.AB与面ACD所成角的余弦值为
D.AB与面ACD所成角的余弦值为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() 的图象与函数
的图象与函数![]() 的图象关于直线
的图象关于直线![]() 对称,则关于函数
对称,则关于函数![]() 以下说法正确的是( )
以下说法正确的是( )
A. 最大值为1,图象关于直线![]() 对称B. 在
对称B. 在![]() 上单调递减,为奇函数
上单调递减,为奇函数
C. 在![]() 上单调递增,为偶函数D. 周期为
上单调递增,为偶函数D. 周期为![]() ,图象关于点
,图象关于点![]() 对称
对称
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com