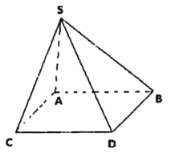
【题目】如图所示，将四棱锥S-ABCD的每一个顶点染上一种颜色，并使同一条棱上的两端异色，如果只有5种色可供使用，则不同的染色方法种数为（ ）
A.240B.360C.420D.960
科目：高中数学 来源： 题型：
【题目】已知函数
的定义域为R，且
的图像过点
.
（1）求实数b的值；
（2）若函数
在
上单调递增，求实数a的取值范围；
（3）是否存在实数a，使函数在R上的最大值为
？若存在，求出a的值；若不存在，请说明理由？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知抛物线C：
=2px经过点
（1，2）．过点Q（0，1）的直线l与抛物线C有两个不同的交点A，B，且直线PA交y轴于M，直线PB交y轴于N．
（Ⅰ）求直线l的斜率的取值范围；
（Ⅱ）设O为原点，
，
，求证：
为定值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】下列四个命题
①函数
与函数
表示同一个函数；
②奇函数的图像一定通过直角坐标系的原点；
③若函数
的定义域为
，则函数
的定义域为
；
④设函数
是在区间
上图像连续的函数，且
，则方程
在区间上至少有一实根；
其中正确命题的序号是（ ）
A.（1）B.（2）C.（3）D.（4）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】我国自改革开放以来，生活越来越好，肥胖问题也目渐显著，为分析肥胖程度对总胆固醇与空腹血糖的影响，在肥胖人群中随机抽出8人，他们的肥胖指数
值、总胆固醇
指标值单位: 
)、空腹血糖
指标值(单位: )如下表所示：
(1)用变量
与
与
的相关系数，分别说明指标值与值、指标值与值的相关程度;
(2)求与的线性回归方程，已知指标值超过5.2为总胆固醇偏高，据此模型分析当值达到多大时，需要注意监控总胆固醇偏高情况的出现(上述数据均要精确到0.01)
参考公式:相关系数
， 
，
.
参考数据: 
，
，
，
，
，
，
，
，
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知直线
的参数方程： 
（
为参数)，曲线
的参数方程： 
（
为参数)，且直线交曲线
于
两点.
(1)将曲线
的参数方程化为普通方程，并求
时， 
的长度；
(2)巳知点
，求当直线倾斜角
变化时， 
的范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
