练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    （本小题10分）已知在三棱锥S--ABC中，∠ACB=900，又SA⊥平面ABC，

    AD⊥SC于D，求证：AD⊥平面SBC，

     

     

     

    【答案】

    证明：SA⊥面ABC， BC⊥面ABC，Þ BC ⊥SA；

    又BC⊥AC，且AC、SA是面SAC内的两相交线，∴BC⊥面SAC；

    又ADÌ面SAC，∴ BC⊥AD，

    又已知SC⊥AD，且BC、SC是面SBC内两相交线，∴ AD⊥面SBC。

    【解析】略

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2010年黑龙江省哈六中高一下学期期中考试数学试题 题型：解答题

    （本小题10分）
    已知等差数列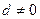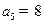，，，且项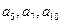分别是某一等比数列中的第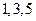项，（1）求数列的第12项； （2）求数列的第项。

    查看答案和解析>>

    科目：高中数学 来源：2011年山东省济南外国语学校高一入学检测数学试卷 题型：解答题

    （本小题10分）
    已知直线  且,求以N(1,1)为圆心,并且与相切的圆的方程.

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年辽宁沈阳二中等重点中学协作体高三领航高考预测（六）理数学卷（解析版） 题型：解答题

    （本小题10分）已知C点在⊙O直径BE的延长线上，CA切⊙O于A 点，CD是∠ACB的平分线且交AE于点F，交AB于点D．

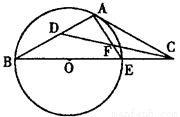
    （1）求∠ADF的度数；

    （2）若AB＝AC，求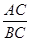的值．

     

    查看答案和解析>>

    科目：高中数学 来源：2014届吉林省高一下学期期末理科数学试卷（解析版） 题型：解答题

    （本小题10分）已知圆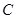经过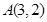、两点，且圆心在直线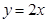上．

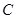    (1) 求圆的方程；

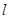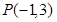    (2) 若直线经过点且与圆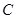相切，求直线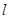的方程．

     

    查看答案和解析>>

    科目：高中数学 来源：甘肃省10-11学年高一下学期期末考试数学 题型：解答题

    （本小题10分）已知，

    （Ⅰ）求；

    （Ⅱ）.

     

     

    查看答案和解析>>

    同步练习册答案