
【题目】《九章算术》是我国古代的数学名著,书中有如下问题:“今有五人分五钱,令上两人所得与下三人等。问各得几何?”其意思是:“已知甲、乙、丙、丁、戊五人分五钱,甲、乙两人所得之和与丙、丁、戊三人所得之和相等,且甲、乙、丙、丁、戊所得依次成等差数列。问五人各得多少钱?”(“钱”是古代的一种重量单位)。这个问题中,戊所得为( )
A. ![]() 钱 B.
钱 B. ![]() 钱 C.
钱 C. ![]() 钱 D.
钱 D. ![]() 钱
钱
科目:高中数学 来源: 题型:
【题目】我校高一年级某研究小组经过调查发现:提高北环隧道的车辆通行能力可有效改善交通状况,在一般情况下,隧道内的车流速度v(单位:千米/小时)是车流密度x(单位:辆/千米,车流密度指每千米道路上车辆的数量)的函数.当隧道内的车流密度达到210辆/千米时,将造成堵塞,此时车流速度为0;当车流密度不超过30辆/千米时,车流速度为60千米/小时,研究表明:当![]() 时,车流速度
时,车流速度![]() 是车流密度
是车流密度![]() 的一次函数.
的一次函数.
(1)求函数![]() 的表达式;
的表达式;
(2)当车流密度为多大时,车流量(单位时间内通过某观测点的车辆数,单位:辆/小时) ![]() 可以达到最大,并求出最大值.
可以达到最大,并求出最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点.

(Ⅰ)证明: BC1//平面A1CD;
(Ⅱ)设AA1= AC=CB=2,AB=2![]() ,求三棱锥C一A1DE的体积.
,求三棱锥C一A1DE的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点A(0,-2),椭圆E: ![]() (a>b>0)的离心率为
(a>b>0)的离心率为![]() ,F是椭圆E的右焦点,直线AF的斜率为
,F是椭圆E的右焦点,直线AF的斜率为![]() ,O为坐标原点.
,O为坐标原点.
(1)求E的方程;
(2)设过点A的动直线l与E相交于P,Q两点.当△OPQ的面积最大时,求l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知边长为4的正三角形ABC的边AB、AC上分别有两点D、E,DE//BC且DE=3,现将△ABC沿DE折成直二面角A﹣DE﹣B,在空间中取一点F使得ADBF为平行四边形,连接AC、FC得六面体ABCEDF,G是BC边上动点.
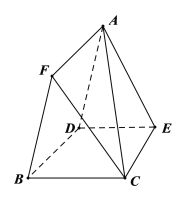
(1)若EG//平面ACF,求CG的长;
(2)若G为BC中点,求二面角G﹣AE﹣D的平面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业有甲、乙两套设备生产同一种产品,为了检测两套设备的生产质量情况,随机从两套设备生产的大量产品中各抽取了50件产品作为样本,检测一项质量指标值,若该项质量指标值落在![]() 内,则为合格品,否则为不合格品.图1是甲套设备的样本的频率分布直方图,表1是乙套设备的样本的频数分布表.
内,则为合格品,否则为不合格品.图1是甲套设备的样本的频率分布直方图,表1是乙套设备的样本的频数分布表.
图1:甲套设备的样本的频率分布直方图

表1:乙套设备的样本的频数分布表
质量指标数 |
|
|
|
|
|
|
频数 |
|
|
|
|
|
|
(1)根据上述所得统计数据,计算产品合格率,并对两套设备的优劣进行比较;
(2)填写下面列联表,并根据列联表判断是否有95%的把握认为该企业生产的这种产品的质量指标值与甲、乙两套设备的选择有关.
甲套设备 | 乙套设备 | 合计 | |
合格 | |||
不合格 | |||
合计 |
附:
|
|
|
|
|
|
|
|
|
|
|
|
![]() 其中
其中![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com