
| x | 2 |
| x |
| x |
| x |
| 2 |


科目:高中数学 来源: 题型:
| a |
| b |
| a |
| b |
| c |
| c |
| a |
| b |
查看答案和解析>>
科目:高中数学 来源: 题型:
判断下列对应是否为集合A到集合B的函数:
(1)A为正实数集,B=R,对于任意的x∈A,x→x的算术平方根;
(2)A={1,2,3,4,5},B={0,2,4,6,8},对于任意的x∈A,x→2x.
查看答案和解析>>
科目:高中数学 来源:2013年山东省高考数学预测试卷(04)(解析版) 题型:填空题
 ,
,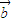 },其中
},其中 ,
, 是不共线向量,B={
是不共线向量,B={ |
| 与
与 ,
, 共面的任意向量},则A和B不可能具有相同的势;
共面的任意向量},则A和B不可能具有相同的势;查看答案和解析>>
科目:高中数学 来源: 题型:
下列描述正确的序号为_______________________________
(1)空集是任何集合的子集 (2)![]() 是幂函数 (3)
是幂函数 (3)![]()
(4)在函数值域中的每一个数,在定义域中都有一个或多个数与之对应
(5)集合![]() ,集合
,集合![]() ,对应关系
,对应关系![]() :每个学生都对应一个班级,那么从集合A到集合B可以构成映射
:每个学生都对应一个班级,那么从集合A到集合B可以构成映射
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com