
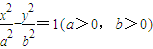 ,其右准线交x轴于点A,双曲线虚轴的下端点为B.过双曲线的右焦点F(c,0)作垂直于x轴的直线交双曲线于点P,若点D满足
,其右准线交x轴于点A,双曲线虚轴的下端点为B.过双曲线的右焦点F(c,0)作垂直于x轴的直线交双曲线于点P,若点D满足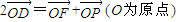 ,
,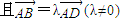 .
.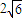 ,求l的方程.
,求l的方程.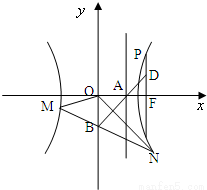
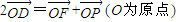 ,可判断D点为FP的中点,再根据
,可判断D点为FP的中点,再根据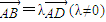 可找到a,b的关系,进而转化为含a,c的等式,即可求出离心率e的值.
可找到a,b的关系,进而转化为含a,c的等式,即可求出离心率e的值.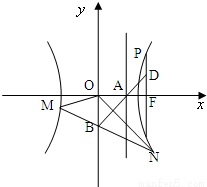 解:(1)∵B(0,-b)
解:(1)∵B(0,-b)
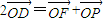 ,即D为线段FP的中点.,
,即D为线段FP的中点.,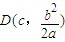
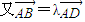 ,即A、B、D共线.
,即A、B、D共线.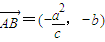 ,
,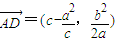 ,
, ,得a=2b,
,得a=2b,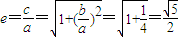
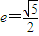 ,∴b2=1,
,∴b2=1,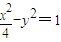 …①
…①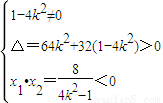 得:
得: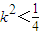
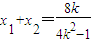
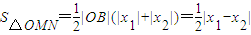 =
=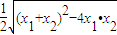 =
=
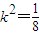 或
或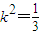 (舍去)
(舍去)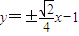


 巧学巧练系列答案
巧学巧练系列答案科目:高中数学 来源: 题型:
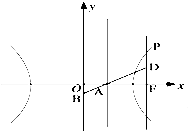 如图,已知双曲线
如图,已知双曲线| x2 |
| a2 |
| y2 |
| b2 |
| OD |
| OF |
| OP |
| AB |
| AD |
| CM |
| CN |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,已知双曲线C1:
如图,已知双曲线C1:| y2 |
| m |
| x2 |
| n |
查看答案和解析>>
科目:高中数学 来源: 题型:
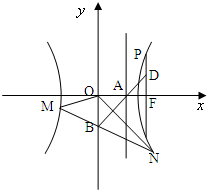 (2008•湖北模拟)如图,已知双曲线
(2008•湖北模拟)如图,已知双曲线| x2 |
| a2 |
| y2 |
| b2 |
| OD |
| OF |
| OP |
| AB |
| AD |
| 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:

(1)求双曲线S的方程;
(2)当k=1时,在双曲线S的上支上求点B,使其与直线l的距离为![]() ;
;
(3)当0≤k<1时,若双曲线S的上支上有且只有一个点B到直线l的距离为![]() ,求斜率k的值及相应的点B的坐标.
,求斜率k的值及相应的点B的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com