则函数
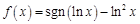的零点个数为（ ）．| A．1 | B．2 | C．3 | D．4 |
科目：高中数学 来源：不详 题型：单选题
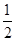x2＋bln(x＋2)在(－1，＋∞)上是减函数，则b的取值范围是( )| A．[－1，＋∞) | B．(－1，＋∞) |
| C．(－∞，－1] | D．(－∞，－1) |
查看答案和解析>>
科目：高中数学 来源：不详 题型：单选题
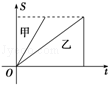
| A．甲比乙先出发 | B．乙比甲跑的路程多 |
| C．甲、乙两人的速度相同 | D．甲比乙先到达终点 |
查看答案和解析>>
科目：高中数学 来源：不详 题型：单选题
立方米，且
. 假设该容器的建造费用仅与其表面积有关. 已知圆柱形部分每平方米建造费用为3千元，半球形部分每平方米建造费用为22千元. 设该容器的建造费用为y千元. 当该容器建造费用最小时，r的值为（ ）
A． | B．1 | C． | D．2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
，
时，
，解得
；当
时，
；当
时，
，即
无解。故函数
的零点有2个。故B正确。
在
处取得最大值，则
在
与
时都取得极值.
的值与函数
的单调区间
，不等式
恒成立，求
的取值范围．
满足
，当
时，
，则函数
上的零点个数为（ ）
存在零点，且对任意
都满足
若关于
的方程
恰有三个不同的根，则实数
的取值范围是
的实数
，关于
的方程
在区间
内（ ）