
【题目】求与直线y= ![]() x+
x+ ![]() 垂直,并且与两坐标轴围成的三角形面积为24的直线l的方程.
垂直,并且与两坐标轴围成的三角形面积为24的直线l的方程.
【答案】解:由直线l与直线y= ![]() x+
x+ ![]() 垂直,可设直线l的方程为y=-
垂直,可设直线l的方程为y=- ![]() x+b,
x+b,
则直线l在x轴,y轴上的截距分别为x0= ![]() b,y0=b.
b,y0=b.
又因为直线l与两坐标轴围成的三角形的面积为24,
所以 ![]()
即 ![]() |
| ![]() b||b|=24,b2=36,
b||b|=24,b2=36,
解得b=6,或b=-6.
故所求的直线方程为y=- ![]() x+6,或y=-
x+6,或y=- ![]() x-6.
x-6.
【解析】先根据直线l与已知直线垂直,可设出直线l的斜截式方程,从而求得直线l在x轴,y轴上的截距,再表示出直线l与两坐标轴围成的三角形的面积,解方程即可求得直线l的方程.
【考点精析】通过灵活运用两条直线垂直与倾斜角、斜率的关系和斜截式方程,掌握两条直线都有斜率,如果它们互相垂直,那么它们的斜率互为负倒数;反之,如果它们的斜率互为负倒数,那么它们互相垂直;直线的斜截式方程:已知直线![]() 的斜率为
的斜率为![]() ,且与
,且与![]() 轴的交点为
轴的交点为![]() 则:
则:![]() 即可以解答此题.
即可以解答此题.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:高中数学 来源: 题型:
【题目】如图,有一直径为8米的半圆形空地,现计划种植果树,但需要有辅助光照.半圆周上的C处恰有一可旋转光源满足果树生长的需要,该光源照射范围是 ![]() ,点E,F在直径AB上,且
,点E,F在直径AB上,且 ![]() .
. 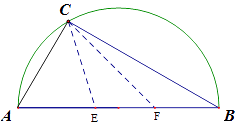
(1)若 ![]() ,求AE的长;
,求AE的长;
(2)设∠ACE=α,求该空地种植果树的最大面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在△ABC中,A,B的坐标分别为(-1,2),(4,3),AC的中点M在y轴上,BC的中点N在x轴上.
(1)求点C的坐标;
(2)求直线MN的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个结论:
①方程k= ![]() 与方程y-2=k(x+1)可表示同一直线;
与方程y-2=k(x+1)可表示同一直线;
②直线l过点P(x1 , y1),倾斜角为 ![]() ,则其方程为x=x1;
,则其方程为x=x1;
③直线l过点P(x1 , y1),斜率为0,则其方程为y=y1;
④所有直线都有点斜式和斜截式方程.
其中正确的个数为( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列各对直线不互相垂直的是( )
A.l1的倾斜角为120°,l2过点P(1,0),Q(4, ![]() )
)
B.l1的斜率为- ![]() ,l2过点P(1,1),Q
,l2过点P(1,1),Q ![]()
C.l1的倾斜角为30°,l2过点P(3, ![]() ),Q(4,2
),Q(4,2 ![]() )
)
D.l1过点M(1,0),N(4,-5),l2过点P(-6,0),Q(-1,3)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点M(2,2),N(5,-2),点P在x轴上,分别求满足下列条件的点P的坐标.
(1)∠MOP=∠OPN(O是坐标原点).
(2)∠MPN是直角.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() .
.
(1)求函数f(x)的单调区间;
(2)若g(x)=xf(x)+mx在区间(0,e]上的最大值为﹣3,求m的值;
(3)若x≥1时,有不等式f(x)≥ ![]() 恒成立,求实数k的取值范围.
恒成立,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义域为R的函数 ![]() 是奇函数.
是奇函数.
(1)求a,b的值;
(2)若对任意的t∈R,不等式f(t2-2t)+f(2t2-k)<0恒成立,求k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com