
【题目】如图,设椭圆![]() :
: ![]() ,长轴的右端点与抛物线
,长轴的右端点与抛物线![]() :
: ![]() 的焦点
的焦点![]() 重合,且椭圆
重合,且椭圆![]() 的离心率是
的离心率是![]() .
.
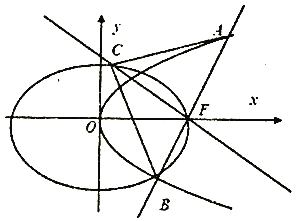
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)过![]() 作直线
作直线![]() 交抛物线
交抛物线![]() 于
于![]() ,
, ![]() 两点,过
两点,过![]() 且与直线
且与直线![]() 垂直的直线交椭圆
垂直的直线交椭圆![]() 于另一点
于另一点![]() ,求
,求![]() 面积的最小值,以及取到最小值时直线
面积的最小值,以及取到最小值时直线![]() 的方程.
的方程.
【答案】(Ⅰ)![]() ; (Ⅱ)
; (Ⅱ)![]() 面积的最小值为9,
面积的最小值为9, ![]() .
.
【解析】试题分析:(Ⅰ)由已知求出抛物线的焦点坐标即得椭圆中的![]() ,再由离心率可求得
,再由离心率可求得![]() ,从而得
,从而得![]() 值,得标准方程;
值,得标准方程;
(Ⅱ)本题考查圆锥曲线中的三角形面积问题,解题方法是设直线![]() 方程为
方程为![]() ,设
,设![]() ,把直线方程代入抛物线方程,化为
,把直线方程代入抛物线方程,化为![]() 的一元二次方程,由韦达定理得
的一元二次方程,由韦达定理得![]() ,由弦长公式得
,由弦长公式得![]() ,同样过
,同样过![]() 与直线
与直线![]() 垂直的直线方程为
垂直的直线方程为![]() ,同样代入椭圆方程,利用韦达定理得
,同样代入椭圆方程,利用韦达定理得![]() ,其中
,其中![]() ,
, ![]() 是
是![]() 点的横坐标,于是可得
点的横坐标,于是可得![]() ,这样就可用
,这样就可用![]() 表示出
表示出![]() 的面积,
的面积,  ,接着可设
,接着可设![]() ,用换元法把
,用换元法把![]() 表示为
表示为![]() 的函数,利用导数的知识可求得最大值.
的函数,利用导数的知识可求得最大值.
试题解析:
(Ⅰ)∵椭圆![]() :
: ![]() ,长轴的右端点与抛物线
,长轴的右端点与抛物线![]() :
: ![]() 的焦点
的焦点![]() 重合,
重合,
∴![]() ,
,
又∵椭圆![]() 的离心率是
的离心率是![]() ,∴
,∴![]() ,
, ![]() ,
,
∴椭圆![]() 的标准方程为
的标准方程为![]() .
.
(Ⅱ)过点![]() 的直线
的直线![]() 的方程设为
的方程设为![]() ,设
,设![]() ,
, ![]() ,
,
联立![]() 得
得![]() ,
,
∴![]() ,
, ![]() ,
,
∴![]() .
.
过![]() 且与直线
且与直线![]() 垂直的直线设为
垂直的直线设为![]() ,
,
联立 得
得![]() ,
,
∴![]() ,故
,故![]() ,
,
∴![]() ,
,
![]() 面积
面积![]() .
.
令![]() ,则
,则![]() ,
,  ,
,
令![]() ,则
,则![]() ,即
,即![]() 时,
时, ![]() 面积最小,
面积最小,
即当![]() 时,
时, ![]() 面积的最小值为9,
面积的最小值为9,
此时直线![]() 的方程为
的方程为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,
, ![]() 是椭圆
是椭圆![]() 上任意一点,且点
上任意一点,且点![]() 到椭圆
到椭圆![]() 的一个焦点的最大距离等于
的一个焦点的最大距离等于![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)若过点![]() 的直线与椭圆
的直线与椭圆![]() 相交于不同两点
相交于不同两点![]() ,设
,设![]() 为椭圆上一点,是否存在整数
为椭圆上一点,是否存在整数![]() ,使得
,使得![]() (其中
(其中![]() 为坐标原点)?若存在,试求整数
为坐标原点)?若存在,试求整数![]() 的所有取值;若不存在,请说明理由.
的所有取值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解某地区心肺疾病是否与性别有关,在某医院随机地对入院
的50人进行了问卷调查,得到了如下的![]() 列联表:
列联表:
患心肺疾病 | 不患心肺疾病 | 合计 | |
男 | 20 | 5 | 25 |
女 | 10 | 15 | 25 |
合计 | 30 | 20 | 50 |
(1)用分层抽样的方法在患心肺疾病的人群中抽取6人,其中男性抽多少人?
(2)在上述抽取的6人中选2人,求恰有一名女性的概率;
(3)为了研究心肺疾病是否与性别有关,请计算出统计量![]() ,判断是否有
,判断是否有![]() 的把握认为
的把握认为
患心肺疾病与性别有关?
右面的临界值表供参考:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式: 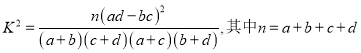 )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com