
【题目】阅读程序框图,该算法的功能是输出( ) 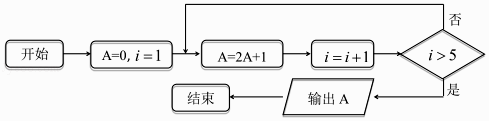
A.数列{2n﹣1}的前 4项的和
B.数列{2n﹣1}的第4项
C.数列{2n}的前5项的和
D.数列{2n﹣1}的第5项
【答案】D
【解析】解:模拟程序的运行,可得: A=0,i=1
执行循环体,A=1=21﹣1,i=2,
不满足条件i>5,执行循环体,A=3=22﹣1,i=3
不满足条件i>5,执行循环体,A=7=23﹣1,i=4
不满足条件i>5,执行循环体,A=15=24﹣1,i=5
不满足条件i>5,执行循环体,A=31=25﹣1,i=6
满足条件i>5,退出循环,输出A的值为31.
观察规律可得该算法的功能是输出数列{2n﹣1}的第5项.
故选:D.
【考点精析】关于本题考查的程序框图,需要了解程序框图又称流程图,是一种用规定的图形、指向线及文字说明来准确、直观地表示算法的图形;一个程序框图包括以下几部分:表示相应操作的程序框;带箭头的流程线;程序框外必要文字说明才能得出正确答案.


 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:高中数学 来源: 题型:
【题目】已知直线l的参数方程为  (t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,圆C的极坐标方程为
(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,圆C的极坐标方程为 ![]() .
.
(Ⅰ)求圆C的直角坐标方程;
(Ⅱ)设点为P(x,y)为直线l与圆C所截得的弦上的动点,求 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线的方程为C:x2=4y,过点Q(0,2)的一条直线与抛物线C交于A,B两点,若抛物线在A,B两点的切线交于点P.
(1)求点P的轨迹方程;
(2)设直线PQ与直线AB的夹角为α,求α的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中,正确的是( ) ①x∈R,2x>3x;②“x≠3”是“|x|≠3”成立的充分条件;③空间中若直线l若平行于平面α,则α内所有直线均与l是异面直线;④空间中有三个角是直角的四边形不一定是平面图形.
A.①③
B.①④
C.②④
D.②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知O为坐标原点,M(x1 , y1),N(x2 , y2)是椭圆 ![]() +
+ ![]() =1上的点,且x1x2+2y1y2=0,设动点P满足
=1上的点,且x1x2+2y1y2=0,设动点P满足 ![]() =
= ![]() +2
+2 ![]()
(Ⅰ)求动点P的轨迹C的方程;
(Ⅱ)若直线l:y=x+m(m≠0)与曲线C交于A,B两点,求三角形OAB面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设正数x,y满足log ![]() x+log3y=m(m∈[﹣1,1]),若不等式3ax2﹣18xy+(2a+3)y2≥(x﹣y)2有解,则实数a的取值范围是( )
x+log3y=m(m∈[﹣1,1]),若不等式3ax2﹣18xy+(2a+3)y2≥(x﹣y)2有解,则实数a的取值范围是( )
A.(1, ![]() ]
]
B.(1, ![]() ]
]
C.[ ![]() ,+∞)
,+∞)
D.[ ![]() ,+∞)
,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,曲线C1的参数方程为 ![]() ,(其中φ为参数),曲线
,(其中φ为参数),曲线 ![]() ,以原点O为极点,x轴的正半轴为极轴建立极坐标系,射线l:θ=α(ρ≥0)与曲线C1 , C2分别交于点A,B(均异于原点O)
,以原点O为极点,x轴的正半轴为极轴建立极坐标系,射线l:θ=α(ρ≥0)与曲线C1 , C2分别交于点A,B(均异于原点O)
(1)求曲线C1 , C2的极坐标方程;
(2)当 ![]() 时,求|OA|2+|OB|2的取值范围.
时,求|OA|2+|OB|2的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com