
分析 (1)利用直线与椭圆相切的性质及其一元二次方程的根与系数的关系即可得出;
(2)设⊙O的切线PQ的方程为:my+t=x,可得$\frac{|t|}{\sqrt{{m}^{2}+1}}$=6,联立$\left\{\begin{array}{l}{my+t=x}\\{{x}^{2}+2{y}^{2}=72}\end{array}\right.$,化为(m2+2)y2+2mty+t2-72=0,△>0,化为36m2+72>t2.利用根与系数的关系及其|PQ|=$\sqrt{(1+{m}^{2})[({y}_{1}+{y}_{2})^{2}-4{y}_{1}{y}_{2}]}$,及其基本不等式的性质即可得出.
解答  解:(1)如图所示,
解:(1)如图所示,
不妨设过点P(3$\sqrt{2}$,3$\sqrt{3}$)的切线方程方程为:y-3$\sqrt{3}$=k(x-3$\sqrt{2}$),
联立$\left\{\begin{array}{l}{{x}^{2}+2{y}^{2}=72}\\{y-3\sqrt{3}=k(x-3\sqrt{2})}\end{array}\right.$,
化为:(1+2k2)x2+12k$(\sqrt{3}-\sqrt{2}k)$x+$18(\sqrt{3}-\sqrt{2}k)^{2}$-72=0,
∵直线与椭圆相切可得:△=144k2$(\sqrt{3}-\sqrt{2}k)^{2}$-4(1+2k2)[$18(\sqrt{3}-\sqrt{2}k)^{2}$-72]=0,
化为6k2+2$\sqrt{6}$k+1=0,
∴k1+k2=-$\frac{\sqrt{6}}{3}$.
(2)设⊙O的切线PQ的方程为:my+t=x,
则$\frac{|t|}{\sqrt{{m}^{2}+1}}$=6,化为t2=36(m2+1).
联立$\left\{\begin{array}{l}{my+t=x}\\{{x}^{2}+2{y}^{2}=72}\end{array}\right.$,化为(m2+2)y2+2mty+t2-72=0,
△=4m2t2-4(m2+2)(t2-72)=4(72m2-2t2+144)>0,化为36m2+72>t2.
∴y1+y2=$\frac{-2mt}{{m}^{2}+2}$,y1y2=$\frac{{t}^{2}-72}{{m}^{2}+2}$.
∴|PQ|=$\sqrt{(1+{m}^{2})[({y}_{1}+{y}_{2})^{2}-4{y}_{1}{y}_{2}]}$=$\sqrt{(1+{m}^{2})[\frac{4{m}^{2}{t}^{2}}{({m}^{2}+2)^{2}}-\frac{4({t}^{2}-72)}{{m}^{2}+2}]}$=$\frac{12\sqrt{2(1+{m}^{2})}}{{m}^{2}+2}$.
设$\sqrt{1+{m}^{2}}$=s≥1,
则|PQ|=$\frac{12\sqrt{2}s}{{s}^{2}+1}$=$\frac{12\sqrt{2}}{s+\frac{1}{s}}$≤6$\sqrt{2}$,当且仅当s=1,即m=0时取等号,满足△>0.
∴线段PQ长度的最大值为6$\sqrt{2}$.
点评 本题考查了椭圆的标准方程及其性质、直线与椭圆相交弦长问题、直线与圆相切的充要条件、点到直线的距离公式、基本不等式的性质,考查了推理能力与计算能力,属于难题.


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案科目:高中数学 来源: 题型:选择题
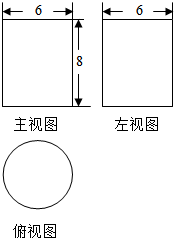 几何体的三视图如图所示,若从该几何体的实心外接球中挖去该几何体,则剩余几何体的表面积是(注:包括外表面积和内表面积)( )
几何体的三视图如图所示,若从该几何体的实心外接球中挖去该几何体,则剩余几何体的表面积是(注:包括外表面积和内表面积)( )| A. | 133π | B. | 100π | C. | 66π | D. | 166π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 男生 | 女生 | 总计 | |
| 看营养说明 | 50 | 30 | 80 |
| 不看营养说明 | 10 | x | y |
| 总计 | 60 | z | 110 |
| P(K2≥K) | 0.10 | 0.05 | 0.01 | 0.005 |
| K | 2.706 | 3.841 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知抛物线C:x2=2py(p>0)的焦点为F(0,1),过点F作直线l交抛物线C于A,B两点.椭圆E的中心在原点,焦点在x轴上,点F是它的一个顶点,且其离心率$e=\frac{{\sqrt{3}}}{2}$.
已知抛物线C:x2=2py(p>0)的焦点为F(0,1),过点F作直线l交抛物线C于A,B两点.椭圆E的中心在原点,焦点在x轴上,点F是它的一个顶点,且其离心率$e=\frac{{\sqrt{3}}}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,F1,F2是椭圆${C_1}:\frac{x^2}{12}+\frac{y^2}{4}=1$与双曲线C2的公共焦点,A,B分别是C1,C2在第二、四象限的公共点.若四边形AF1BF2为矩形,则C2的离心率是$\sqrt{2}$.
如图,F1,F2是椭圆${C_1}:\frac{x^2}{12}+\frac{y^2}{4}=1$与双曲线C2的公共焦点,A,B分别是C1,C2在第二、四象限的公共点.若四边形AF1BF2为矩形,则C2的离心率是$\sqrt{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com