
【题目】如图:双曲线![]() :
:![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,过
,过![]() 作直线
作直线![]() 交
交![]() 轴于点
轴于点![]() .
.
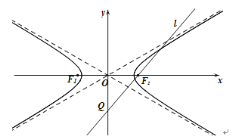
(1)当直线![]() 平行于
平行于![]() 的一条渐近线时,求点
的一条渐近线时,求点![]() 到直线
到直线![]() 的距离;
的距离;
(2)当直线![]() 的斜率为
的斜率为![]() 时,在
时,在![]() 的右支上是否存在点
的右支上是否存在点![]() ,满足
,满足![]() ?若存在,求出
?若存在,求出![]() 点的坐标;若不存在,说明理由;
点的坐标;若不存在,说明理由;
(3)若直线![]() 与
与![]() 交于不同两点
交于不同两点![]() 、
、![]() ,且
,且![]() 上存在一点
上存在一点![]() ,满足
,满足![]() (其中
(其中![]() 为坐标原点),求直线
为坐标原点),求直线![]() 的方程.
的方程.
【答案】(1)![]() (2)在双曲线
(2)在双曲线![]() 的右支上不存在点
的右支上不存在点![]() ,满足
,满足![]() ,详见解析(3)
,详见解析(3)![]()
【解析】
(1) 双曲线![]() :
:![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 的渐近线方程为
的渐近线方程为![]() ,由对称性可知
,由对称性可知![]() :
:![]() ,根据点到直线的距离公式,即可求得答案;
,根据点到直线的距离公式,即可求得答案;
(2) 直线![]() 的斜率为
的斜率为![]() 时,
时,![]() 的方程为
的方程为![]() ,设
,设![]() 右支上的点
右支上的点![]() 的坐标为
的坐标为![]() ,则
,则![]() ,由
,由![]() ,得
,得![]() ,结合已知,即可求得答案;
,结合已知,即可求得答案;
(3) 设![]() :
:![]() ,联立
,联立![]() 与
与![]() 的方程,得
的方程,得![]() ,根据韦达定理,结合已知,即可求得答案.
,根据韦达定理,结合已知,即可求得答案.
(1)![]() 双曲线
双曲线![]() :
:![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]()
![]() ,
,![]() ,
,![]() 的渐近线方程为
的渐近线方程为![]() ,
,
由对称性可知![]() :
:![]() ,即
,即![]() ,
,
![]()
![]() 到
到![]() 的距离
的距离![]() .
.
(2)当直线![]() 的斜率为
的斜率为![]() 时,
时,![]() 的方程为
的方程为![]() ,故
,故![]() ,
,
又![]()
![]() ,故
,故![]() ,
,
设![]() 右支上的点
右支上的点![]() 的坐标为
的坐标为![]() ,则
,则![]() ,
,
由![]() ,得
,得![]() ,即:
,即:![]()
由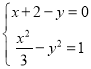 消去
消去![]()
得![]() ,
,
由根与系数的关系知,此方程无正根
![]() 在双曲线
在双曲线![]() 的右支上不存在点
的右支上不存在点![]() ,满足
,满足![]() .
.
(3)设![]() ,
,![]() ,则
,则![]() ,
,
由![]() 点在曲线上,故
点在曲线上,故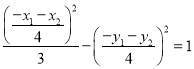
![]() ①
①
设![]() :
:![]() .
.
联立![]() 与
与![]() 的方程,得
的方程,得![]() ,
,
由于![]() 与
与![]() 交于不同两点,
交于不同两点,
![]()
![]() ,
,
![]()
![]() ,
,
从而①即为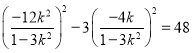 ,
,
![]() 解得
解得![]() .
.
即直线![]() 的方程为
的方程为![]() .
.


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,圆
中,圆![]() ,以坐标原点
,以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴,直线
轴正半轴为极轴,直线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 交圆
交圆![]() 于
于![]() 两点,
两点,![]() 为
为![]() 中点.
中点.
(1)求点![]() 轨迹的极坐标方程;
轨迹的极坐标方程;
(2)若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,A,B为椭圆![]() 的左、右顶点,直线
的左、右顶点,直线![]() 过椭圆C的右焦点F且交椭圆于P,Q两点.连结
过椭圆C的右焦点F且交椭圆于P,Q两点.连结![]() 并延长交直线
并延长交直线![]() 于点M.
于点M.
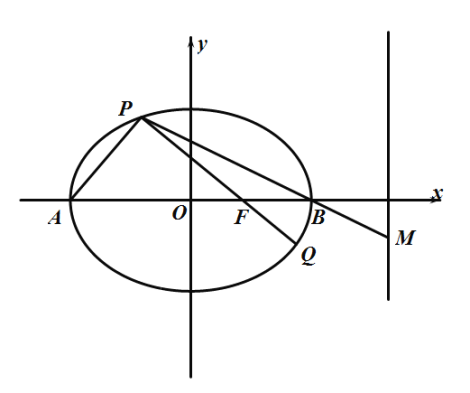
(1)若直线![]() 的斜率为
的斜率为![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)求证:A,Q,M三点共线.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】河北省高考综合改革从2018年秋季入学的高一年级学生开始实施,新高考将实行“3+1+2”模式,其中3表示语文、数学、外语三科必选,1表示从物理、历史两科中选择一科,2表示从化学、生物、政治、地理四科中选择两科.某校2018级入学的高一学生选科情况如下表:
选科组合 | 物化生 | 物化政 | 物化地 | 物生政 | 物生地 | 物政地 | 史政地 | 史政化 | 史生政 | 史地化 | 史地生 | 史化生 | 合计 |
男 | 130 | 45 | 55 | 30 | 25 | 15 | 30 | 10 | 40 | 10 | 15 | 20 | 425 |
女 | 100 | 45 | 50 | 35 | 35 | 35 | 40 | 20 | 55 | 15 | 25 | 20 | 475 |
合计 | 230 | 90 | 105 | 65 | 60 | 50 | 70 | 30 | 95 | 25 | 40 | 40 | 900 |
(1)完成下面的![]() 列联表,并判断是否在犯错误概率不超过0.01的前提下,认为“选择物理与学生的性别有关”?
列联表,并判断是否在犯错误概率不超过0.01的前提下,认为“选择物理与学生的性别有关”?
(2)以频率估计概率,从该校2018级高一学生中随机抽取3名同学,设这三名同学中选择物理的人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
选择物理 | 不选择物理 | 合计 | |
男 | 425 | ||
女 | 475 | ||
合计 | 900 |
附表及公式: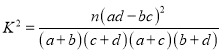
| 0.150 | 0.100 | 0.050 | 0.010 |
| 2.072 | 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线C的参数方程为![]() ,(θ为参数),以原点为极点,x轴非负半轴为极轴建立极坐标系.
,(θ为参数),以原点为极点,x轴非负半轴为极轴建立极坐标系.
(1)求曲线C的极坐标方程;
(2)在平面直角坐标系xOy中,A(﹣2,0),B(0,﹣2),M是曲线C上任意一点,求△ABM面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是国家统计局给出的2014年至2018年我国城乡就业人员数量的统计图表,结合这张图表,以下说法错误的是( )
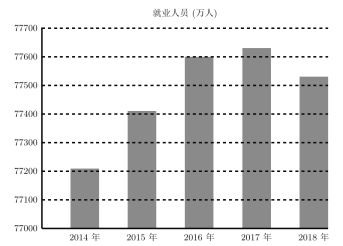
A.2017年就业人员数量是最多的
B.2017年至2018年就业人员数量呈递减状态
C.2016年至2017年就业人员数量与前两年比较,增加速度减缓
D.2018年就业人员数量比2014年就业人员数量增长超过400万人
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 为两个随机事件,给出以下命题:(1)若
为两个随机事件,给出以下命题:(1)若![]() 为互斥事件,且
为互斥事件,且![]() ,
,![]() ,则
,则![]() ;(2)若
;(2)若![]() ,
,![]() ,
,![]() ,则
,则![]() 为相互独立事件;(3)若
为相互独立事件;(3)若![]() ,
,![]() ,
,![]() ,则
,则![]() 为相互独立事件;(4)若
为相互独立事件;(4)若![]() ,
,![]() ,
,![]() ,则
,则![]() 为相互独立事件;(5)若
为相互独立事件;(5)若![]() ,
,![]() ,
,![]() ,则
,则![]() 为相互独立事件;其中正确命题的个数为( )
为相互独立事件;其中正确命题的个数为( )
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() (
(![]() )的一个焦点
)的一个焦点![]() 与抛物线
与抛物线![]() :
:![]() 的焦点重合,且离心率为
的焦点重合,且离心率为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)过焦点![]() 的直线
的直线![]() 与抛物线
与抛物线![]() 交于
交于![]() ,
,![]() 两点,与椭圆
两点,与椭圆![]() 交于
交于![]() ,
,![]() 两点,满足
两点,满足![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设中心在原点O,焦点在x轴上的椭圆C过点![]() ,F为C的右焦点,⊙F的方程为
,F为C的右焦点,⊙F的方程为![]()
(1)求C的方程;
(2)若直线![]()
![]() 与⊙O相切,与⊙F交于M、N两点,与C交于P、Q两点,其中M、P在第一象限,记⊙O的面积为
与⊙O相切,与⊙F交于M、N两点,与C交于P、Q两点,其中M、P在第一象限,记⊙O的面积为![]() ,求
,求![]() 取最大值时,直线l的方程.
取最大值时,直线l的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com