
【题目】定义:若两个椭圆的离心率相等,则称两个椭圆是“相似”的,如图,椭圆![]() 与椭圆
与椭圆![]() 是相似的两个椭圆,并且相交于上下两个顶点,椭圆
是相似的两个椭圆,并且相交于上下两个顶点,椭圆![]() 的长轴长是4,椭圆
的长轴长是4,椭圆![]() ,短轴长是1,点
,短轴长是1,点![]() ,
,![]() 分别是椭圆
分别是椭圆![]() 的左焦点与右焦点.
的左焦点与右焦点.

(1)求椭圆![]() ,
,![]() 的方程;
的方程;
(2)过![]() 的直线交椭圆
的直线交椭圆![]() 于点
于点![]() ,
,![]() ,求
,求![]() 面积的最大值.
面积的最大值.
科目:高中数学 来源: 题型:
【题目】如图,在梯形![]() 中,
中, ![]() ,
, ![]() .
. ![]() ,且
,且![]() 平面
平面![]() ,
, ![]() ,点
,点![]() 为
为![]() 上任意一点.
上任意一点.
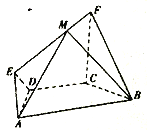
(1)求证: ![]() ;
;
(2)点![]() 在线段
在线段![]() 上运动(包括两端点),若平面
上运动(包括两端点),若平面![]() 与平面
与平面![]() 所成的锐二面角为60°,试确定点
所成的锐二面角为60°,试确定点![]() 的位置.
的位置.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右顶点分别为
的左、右顶点分别为![]() ,左焦点为
,左焦点为![]() ,点
,点![]() 为椭圆
为椭圆![]() 上任一点,若直线
上任一点,若直线![]() 与
与![]() 的斜率之积为
的斜率之积为![]() ,且椭圆
,且椭圆![]() 经过点
经过点![]() .
.
(1)求椭圆的方程;
(2)若![]() 交直线
交直线![]() 于
于![]() 两点,过左焦点
两点,过左焦点![]() 作以
作以![]() 为直径的圆的切线.问切线长是否为定值,若是,请求出定值;若不是,请说明理由.
为直径的圆的切线.问切线长是否为定值,若是,请求出定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市举行“中学生诗词大赛”,分初赛和复赛两个阶段进行,规定:初赛成绩大于90分的具有复赛资格,某校有800名学生参加了初赛,所有学生的成绩均在区间![]() 内,其频率分布直方图如图.
内,其频率分布直方图如图.

(Ⅰ)求获得复赛资格的人数;
(Ⅱ)从初赛得分在区间![]() 的参赛者中,利用分层抽样的方法随机抽取
的参赛者中,利用分层抽样的方法随机抽取![]() 人参加学校座谈交流,那么从得分在区间
人参加学校座谈交流,那么从得分在区间![]() 与
与![]() 各抽取多少人?
各抽取多少人?
(Ⅲ)从(Ⅱ)抽取的![]() 人中,选出
人中,选出![]() 人参加全市座谈交流,设
人参加全市座谈交流,设![]() 表示得分在区间
表示得分在区间![]() 中参加全市座谈交流的人数,求
中参加全市座谈交流的人数,求![]() 的分布列及数学期望E(X).
的分布列及数学期望E(X).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,离心率
,离心率![]() .左焦点为
.左焦点为![]() ,过点
,过点![]() 且与
且与![]() 轴垂直的直线被椭圆截得的线段长为3.
轴垂直的直线被椭圆截得的线段长为3.
(1)求该椭圆的方程;
(2)过椭圆的左焦点的任意一条直线![]() 与椭圆交于
与椭圆交于![]() 两点,在
两点,在![]() 轴上是否存在定点
轴上是否存在定点![]() 使得
使得![]() 轴平分
轴平分![]() ,若存在,求出定点坐标,若不存在,说明理由.
,若存在,求出定点坐标,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱![]() 中,D为A1B1的中点,AB=BC=2,
中,D为A1B1的中点,AB=BC=2,![]() ,
,![]() ,则异面直线BD与AC所成的角为( )
,则异面直线BD与AC所成的角为( )

A. 30°B. 45°C. 60°D. 90°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 过点
过点![]() ,离心率为
,离心率为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)![]() ,
, ![]() 是过点
是过点![]() 且互相垂直的两条直线,其中
且互相垂直的两条直线,其中![]() 交圆
交圆![]() 于
于![]() ,
, ![]() 两点,
两点, ![]() 交椭圆
交椭圆![]() 于另一个点
于另一个点![]() ,求
,求![]() 面积取得最大值时直线
面积取得最大值时直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场销售某种品牌的空调器,每周周初购进一定数量的空调器,商场每销售一台空调器可获利500元,若供大于求,则每台多余的空调器需交保管费100元;若供不应求,则可从其他商店调剂供应,此时每台空调器仅获利润200元。
(Ⅰ)若该商场周初购进20台空调器,求当周的利润(单位:元)关于当周需求量n(单位:台,![]() )的函数解析式
)的函数解析式![]() ;
;
(Ⅱ)该商场记录了去年夏天(共10周)空调器需求量n(单位:台),整理得下表:
周需求量n | 18 | 19 | 20 | 21 | 22 |
频数 | 1 | 2 | 3 | 3 | 1 |
以10周记录的各需求量的频率作为各需求量发生的概率,若商场周初购进20台空调器,X表示当周的利润(单位:元),求X的分布列及数学期望。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点A(t,1)为函数y=ax2+bx+4(a,b为常数,且a≠0)与y=x图象的交点.
(1)求t;
(2)若函数y=ax2+bx+4的图象与x轴只有一个交点,求a,b;
(3)若1≤a≤2,设当![]() ≤x≤2时,函数y=ax2+bx+4的最大值为m,最小值为n,求m﹣n的最小值.
≤x≤2时,函数y=ax2+bx+4的最大值为m,最小值为n,求m﹣n的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com