
(本小题满分14分)已知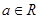 且
且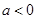 ,设函数
,设函数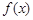 = ax2 +x-3alnx.
= ax2 +x-3alnx.
(I)求函数 的单调区间;
的单调区间;
(II)当a=-1时,证明: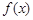 ≤2x-2.
≤2x-2.
(I) 的单调递增区间为(0,
的单调递增区间为(0,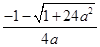 )、递减区间为(
)、递减区间为(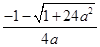 ,
,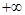 ); (II)见解析。
); (II)见解析。
解析试题分析:(I)先求出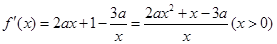 ,然后再根据导数大于(小于)零,分别求出其单调增(减)区间.
,然后再根据导数大于(小于)零,分别求出其单调增(减)区间.
(II)当a=-1时,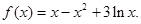 ,然后构造函数
,然后构造函数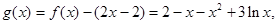 再利用导数求g(x)的最大值,证明其最大值不大于零即可.
再利用导数求g(x)的最大值,证明其最大值不大于零即可.
(I) 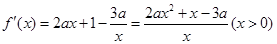 …………………………1分
…………………………1分
令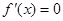 解得
解得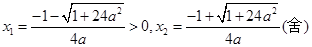 …………………3分
…………………3分
列表如下:
…………………6分x (0, 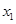 )
) ( 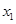 ,
,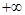 )
)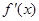
+ - 


故 的单调递增区间为(0,
的单调递增区间为(0,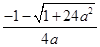 )、递减区间为(
)、递减区间为(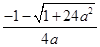 ,
,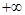 )…………………7分
)…………………7分
(II)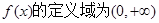 ,a=-1时,
,a=-1时,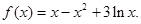
设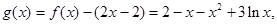 ………………………………9分
………………………………9分
则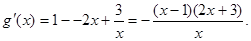 ……………………10分
……………………10分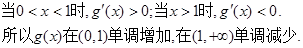 ……………………12分
……………………12分
而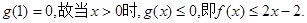 ……………………14分
……………………14分
考点:导数在研究函数的单调性,极值,最值,证明不等式中的应用.
点评:利用导数求单调区间时:如果含有参数,要注意分类讨论,并且要注意函数的定义域.
证明不等式的问题可以通过构造函数,通过导数研究函数的最值证明不等式是常用的策略之一.


科目:高中数学 来源: 题型:解答题
(本题满分16分)某公司将进货单价为8元一个的商品按10元一个销售,每天可卖出100个,若这种商品的销售价每个上涨1元,则销售量就减少10个.
(1)求函数解析式;
(1)求销售价为13元时每天的销售利润;
(2)如果销售利润为360元,那么销售价上涨了几元?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)设某物体一天中的温度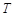 是时间
是时间 的函数:
的函数: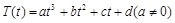 ,其中温度的单位是
,其中温度的单位是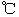 ,时间单位是小时,
,时间单位是小时,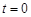 表示12:00,
表示12:00, 取正值表示12:00以后.若测得该物体在8:00的温度是
取正值表示12:00以后.若测得该物体在8:00的温度是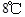 ,12:00的温度为
,12:00的温度为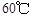 ,13:00的温度为
,13:00的温度为 ,且已知该物体的温度在8:00和16:00有相同的变化率.
,且已知该物体的温度在8:00和16:00有相同的变化率.
(1)写出该物体的温度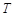 关于时间
关于时间 的函数关系式;
的函数关系式;
(2)该物体在10:00到14:00这段时间中(包括10:00和14:00),何时温度最高,并求出最高温度;
(3)如果规定一个函数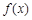 在区间
在区间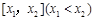 上的平均值为
上的平均值为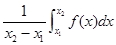 ,求该物体在8:00到16:00这段时间内的平均温度.
,求该物体在8:00到16:00这段时间内的平均温度.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题12分)某产品原来的成本为1000元/件,售价为1200元/件,年销售量为1万件。由于市场饱和顾客要求提高,公司计划投入资金进行产品升级。据市场调查,若投入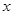 万元,每件产品的成本将降低
万元,每件产品的成本将降低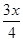 元,在售价不变的情况下,年销售量将减少
元,在售价不变的情况下,年销售量将减少 万件,按上述方式进行产品升级和销售,扣除产品升级资金后的纯利润记为
万件,按上述方式进行产品升级和销售,扣除产品升级资金后的纯利润记为 (单位:万元).(纯利润=每件的利润×年销售量-投入的成本)
(单位:万元).(纯利润=每件的利润×年销售量-投入的成本)
(Ⅰ)求 的函数解析式;
的函数解析式;
(Ⅱ)求 的最大值,以及
的最大值,以及 取得最大值时
取得最大值时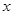 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com