练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知是底面边长为的正四棱柱，是和的交点.

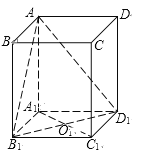
    （1）若正四棱柱的高与底面边长相等，求二面角的大小（结果用反三角函数值表示）；

    （2）若点到平面的距离为，求正四棱柱的高.

    【答案】（1）；（2）.

    【解析】

    （1）由题意，正四棱柱是棱长为1的正方体，连结，则是二面角的平面角，由此能求出二面角的大小.
    （2）设正四棱柱的高为，以为原点，为轴，为轴，为轴，建立空间直角坐标系，利用向量法能求出正四棱柱的高.

    （1）由题意，正四棱柱是棱长为的正方体，

    连结，因为，为的中点，所以，

    又，所以是二面角的平面角.

    因为平面，所以，

    所以，.　

    所以，二面角的大小为；

    （2）设正四棱柱的高为.

    以为原点，为轴，为轴，为轴，建立空间直角坐标系，

    则，，，，

    ，，.

    设平面一个法向量为，

    由得即

    取，得，　

    所以，点以平面的距离为，　

    解得.　　

    所以，正四棱柱的高为.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】设函数．

    （Ⅰ）当时，求曲线在点处的切线方程；

    （Ⅱ）设，若对任意的，存在使得成立，求的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设和是双曲线上的两点，线段的中点为，直线不经过坐标原点．

    （1）若直线和直线的斜率都存在且分别为和，求证：；

    （2）若双曲线的焦点分别为、，点的坐标为，直线的斜率为，求由四点、、、所围成四边形的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】甲乙两队参加听歌猜歌名游戏，每队人.随机播放一首歌曲， 参赛者开始抢答，每人只有一次抢答机会，答对者为本队赢得一分，答错得零分， 假设甲队中每人答对的概率均为，乙队中人答对的概率分别为，且各人回答正确与否相互之间没有影响.

    (1)若比赛前随机从两队的个选手中抽取两名选手进行示范，求抽到的两名选手在同一个队的概率;

    (2)用表示甲队的总得分，求随机变量的分布列和数学期望;

    (3)求两队得分之和大于4的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知是定义在上的函数，满足.

    （1）证明：2是函数的周期；

    （2）当时，，求在时的解析式，并写出在（）时的解析式；

    （3）对于（2）中的函数，若关于x的方程恰好有20个解，求实数a的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设、是关于的方程的两个不相等的实数根，那么过两点、的直线与圆的位置关系是（ ）

    A.相离B.相切C.相交D.随的变化而变化

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，则直线y=x+1与曲线的交点个数为_____；若关于x的方程有三个不等实根，则实数a的取值范围是_____.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】关于函数，下列说法正确的是( )

    （1）是的极小值点；

    （2）函数有且只有1个零点；

    （3）恒成立；

    （4）设函数，若存在区间，使在上的值域是，则.

    A.(1) (2)B.(2)(4)C.(1) (2) (4)D.(1)(2)(3)(4)

    查看答案和解析>>

    同步练习册答案