
【题目】椭圆C:![]() 的离心率是
的离心率是![]() ,过焦点且垂直于x轴的直线被椭圆截得的弦长为
,过焦点且垂直于x轴的直线被椭圆截得的弦长为![]() .
.
![]() 求椭圆C的方程;
求椭圆C的方程;
![]() 过点
过点![]() 的动直线l与椭圆C相交于A,B两点,在y轴上是否存在异于点P的定点Q,使得直线l变化时,总有
的动直线l与椭圆C相交于A,B两点,在y轴上是否存在异于点P的定点Q,使得直线l变化时,总有![]() ?若存在,求点Q的坐标;若不存在,说明理由.
?若存在,求点Q的坐标;若不存在,说明理由.
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,以坐标原点
中,以坐标原点![]() 为极点,
为极点, ![]() 轴正半轴为极轴建立极坐标系,已知曲线
轴正半轴为极轴建立极坐标系,已知曲线![]() 的极坐标方程为:
的极坐标方程为: ![]() ,直线
,直线![]() 的参数方程是
的参数方程是![]() (
(![]() 为参数,
为参数, ![]() ).
).
(1)求曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设直线![]() 与曲线
与曲线![]() 交于两点
交于两点![]() ,且线段
,且线段![]() 的中点为
的中点为![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 、
、![]() 分别为椭圆
分别为椭圆![]() 的左右顶点,设点
的左右顶点,设点![]() 为直线
为直线![]() 上不同于点
上不同于点![]() 的任意一点,若直线
的任意一点,若直线![]() 、
、![]() 分别与椭圆相交于异于
分别与椭圆相交于异于![]() 、
、![]() 的点
的点![]() 、
、![]() .
.
(1)判断![]() 与以
与以![]() 为直径的圆的位置关系(内、外、上)并证明.
为直径的圆的位置关系(内、外、上)并证明.
(2)记直线![]() 与轴的交点为
与轴的交点为![]() ,在直线
,在直线![]() 上,求点
上,求点![]() ,使得
,使得![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了研究某药品的疗效,选取若干名志愿者进行临床试验,所有志愿者的舒张压数据(单位:kPa)的分组区间为[12,13),[13,14),[14,15),[15,16),[16,17],将其按从左到右的顺序分别编号为第一组,第二组,![]() ,第五组,右图是根据试验数据制成的频率分布直方图,已知第一组与第二组共有20人,第三组中没有疗效的有6人,则第三组中有疗效的人数为( )
,第五组,右图是根据试验数据制成的频率分布直方图,已知第一组与第二组共有20人,第三组中没有疗效的有6人,则第三组中有疗效的人数为( )
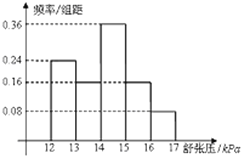
A. 6 B. 8 C. 12 D. 18
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于以下四个命题:①两条异面直线有无数条公垂线;②直线在平面内的射影是直线;③如果两条直线在同一个平面内的射影平行,那这两条直线平行;④过两条异面直线的一条有且仅有一个平面与已知直线平行;上述命题中为真命题的个数为( )个
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com