
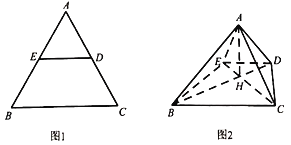
【题目】如图1,在边长为2的等边△ABC中,D,E分别为边AC,AB的中点.将△ADE沿DE折起,使得AB⊥AD,得到如图2的四棱锥A﹣BCDE,连结BD,CE,且BD与CE交于点H.
(1)证明:![]() ;
;
(2)设点B到平面AED的距离为h1,点E到平面ABD的距离为h2,求![]() 的值.
的值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)在图1中,证明BD⊥AC,ED∥BC,则在图2中,有![]() ,得DH
,得DH![]() ,然后证明△BAD∽△AHD,可得∠AHD=∠BAD=90°,即AH⊥BD;
,然后证明△BAD∽△AHD,可得∠AHD=∠BAD=90°,即AH⊥BD;
(2)由VB﹣AED=VE﹣ABD,得![]() ,分别求出三角形ABD与三角形AED的面积得答案.
,分别求出三角形ABD与三角形AED的面积得答案.
(1)证明:在图1中,∵△ABC为等边三角形,且D为边AC的中点,∴BD⊥AC,
在△BCD中,BD⊥CD,BC=2,CD=1,∴BD![]() ,
,
∵D、E分别为边AC、AB的中点,∴ED∥BC,
在图2中,有![]() ,∴DH
,∴DH![]() .
.
在Rt△BAD中,BD![]() ,AD=1,
,AD=1,
在△BAD和△AHD中,∵![]() ,∠BDA=∠ADH
,∠BDA=∠ADH
∴△BAD∽△AHD.
∴∠AHD=∠BAD=90°,即AH⊥BD;
(2)解:∵VB﹣AED=VE﹣ABD,
∴![]() ,则
,则![]() .
.
∵△AED是边长为1的等边三角形,∴![]() .
.
在Rt△ABD中,BD![]() ,AD=1,则AB
,AD=1,则AB![]() .
.
∴![]() ,
,
则![]() .
.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案科目:高中数学 来源: 题型:
【题目】2018年俄罗斯世界杯共有32支球队参赛,将32支球队分为8个小组,每个小组有4支球队,各个小组首先进行小组赛,小组赛采用单循环制,即小组内的每支球队都与本小组的其他球队进行一场比赛,球迷小王喜欢的4支球队分别为西班牙队、法国队、德国队和韩国队,其中西班牙队在B组,法国队在C组,德国队和韩国队同在F组.小王要从自己喜欢的4支球队的所有小组赛中,选择5场比赛观看,则至少观看2场法国队比赛的方法有_____________种.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】双纽线最早于1694年被瑞士数学家雅各布·伯努利用来描述他所发现的曲线.在平面直角坐标系![]() 中,把到定点
中,把到定点![]() ,
,![]() 距离之积等于
距离之积等于![]() 的点的轨迹称为双纽线
的点的轨迹称为双纽线![]() .已知点
.已知点![]() 是双纽线
是双纽线![]() 上一点,下列说法中正确的有( )
上一点,下列说法中正确的有( )
①双纽线经过原点![]() ; ②双纽线
; ②双纽线![]() 关于原点
关于原点![]() 中心对称;
中心对称;
③![]() ; ④双纽线
; ④双纽线![]() 上满足
上满足![]() 的点
的点![]() 有两个.
有两个.
A.①②B.①②③C.②③D.②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() ,
, ![]()
(1)若![]() ,且
,且![]() 在其定义域上存在单调递减区间,求实数
在其定义域上存在单调递减区间,求实数![]() 的取值范围;
的取值范围;
(2)设函数![]() ,
, ![]() ,若
,若![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)设函数![]() 的图象
的图象![]() 与函数
与函数![]() 的图象
的图象![]() 交于点
交于点![]() 、
、![]() ,过线段
,过线段![]() 的中点作
的中点作![]() 轴的垂线分别交
轴的垂线分别交![]() ,
, ![]() 于点
于点![]() 、
、![]() ,证明:
,证明: ![]() 在点
在点![]() 处的切线与
处的切线与![]() 在点
在点![]() 处的切线不平行.
处的切线不平行.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中正确的是( )
A.对具有线性相关关系的变量![]() 有一组观测数据
有一组观测数据![]() ,其线性回归方程是
,其线性回归方程是![]() ,且
,且![]() ,则实数
,则实数![]() 的值是
的值是![]()
B.正态分布![]() 在区间
在区间![]() 和
和![]() 上取值的概率相等
上取值的概率相等
C.若两个随机变量的线性相关性越强,则相关系数![]() 的值越接近于1
的值越接近于1
D.若一组数据![]() 的平均数是2,则这组数据的众数和中位数都是2
的平均数是2,则这组数据的众数和中位数都是2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以坐标原点为极点,
为参数).以坐标原点为极点,![]() 轴的非负半轴为极轴建立极坐标系,曲线
轴的非负半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)将![]() 的方程化为普通方程,将
的方程化为普通方程,将![]() 的方程化为直角坐标方程;
的方程化为直角坐标方程;
(2)已知直线![]() 的参数方程为
的参数方程为![]() (
(![]() ,
,![]() 为参数,且
为参数,且![]() ),
),![]() 与
与![]() 交于点
交于点![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com