Question

14．某校高三在2014年的“武汉市二月调考”中有1000人参加考试，数学考试的成绩ξ～N（90，a²）（a＞0，试卷满分150分），统计结果显示数学考试成绩在70分到110分之间的人数约为总人数的$\frac{4}{5}$，则此次数学考试成绩不低于110分的学生约有100人．

Answer 1

分析 先根据正态分布曲线的图象特征，关注其对称性画出函数的图象，观察图象在70分到110分之间的人数概率，即可得成绩不低于110分的学生人数概率，最后即可求得成绩不低于110分的学生数．

解答 解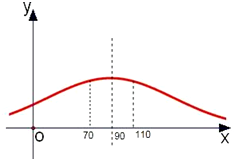：∵成绩ξ～N（90，a²），
∴其正态曲线关于直线x=90对称，
又∵成绩在70分到110分之间的人数约为总人数的$\frac{4}{5}$，
由对称性知：
成绩在110分以上的人数约为总人数的$\frac{1}{2}$（1-$\frac{4}{5}$）=$\frac{1}{10}$，
∴此次数学考试成绩不低于110分的学生约有：$\frac{1}{10}×1000$=100．
故答案为：100．

点评 本小题主要考查正态分布曲线的特点及曲线所表示的意义等基础知识，考查运算求解能力，考查数形结合思想、化归与转化思想．属于基础题．正态分布是概率论中最重要的一种分布，也是自然界最常见的一种分布．该分布由两个参数--平均值和方差决定．概率密度函数曲线以均值为对称中线，方差越小，分布越集中在均值附近．