
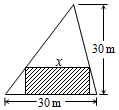
 在如图所示的三角形空地中,欲建一个面积不小于200m2的内接矩形花园(阴影部分),则其边长x(单位:m)的取值范围是[10,20].
在如图所示的三角形空地中,欲建一个面积不小于200m2的内接矩形花园(阴影部分),则其边长x(单位:m)的取值范围是[10,20]. 分析 设矩形的另一边长为ym,由相似三角形的性质可得:$\frac{x}{30}$=$\frac{30-y}{30}$,(0<x<30).矩形的面积S=x(30-x),利用S≥200解出即可.
解答 解:设矩形的另一边长为ym,
由相似三角形的性质可得:$\frac{x}{30}$=$\frac{30-y}{30}$,
解得y=30-x,(0<x<30)
∴矩形的面积S=x(30-x),
∵矩形花园的面积不小于200m2,
∴x(30-x)≥200,
化为(x-10)(x-20)≤0,解得10≤x≤20.
满足0<x<30.
故其边长x(单位m)的取值范围是[10,20].
故答案为:[10,20].
点评 本题考查了相似三角形的性质、三角形的面积计算公式、一元二次不等式的解法等基础知识与基本技能方法,属于基础题.


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:高中数学 来源: 题型:解答题
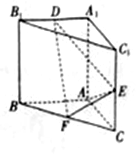 三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AA1=AB=AC=1,E、F分别是CC1、BC的中点,AE⊥A1B1
三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AA1=AB=AC=1,E、F分别是CC1、BC的中点,AE⊥A1B1查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
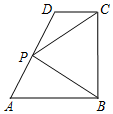 如图,在直角梯形ABCD中,AB∥CD,AB⊥BC,AB=2,CD=1,BC=a(a>0),P为线段AD(含端点)上一个动点,设$\overrightarrow{AP}=x\overrightarrow{AD}$,$\overrightarrow{PB}•\overrightarrow{PC}=y$,则得到函数y=f(x).
如图,在直角梯形ABCD中,AB∥CD,AB⊥BC,AB=2,CD=1,BC=a(a>0),P为线段AD(含端点)上一个动点,设$\overrightarrow{AP}=x\overrightarrow{AD}$,$\overrightarrow{PB}•\overrightarrow{PC}=y$,则得到函数y=f(x).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | sinθ-cosθ | B. | cosθ-sinθ | C. | ±(sinθ-cosθ) | D. | sinθ+cosθ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4$\sqrt{2}$ | B. | $\sqrt{5}$ | C. | 3 | D. | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com