
【题目】关于函数![]() 有下述四个结论:①若
有下述四个结论:①若![]() ,则
,则![]() ;②
;②![]() 的图象关于点
的图象关于点![]() 对称;③函数
对称;③函数![]() 在
在![]() 上单调递增;④
上单调递增;④![]() 的图象向右平移
的图象向右平移![]() 个单位长度后所得图象关于
个单位长度后所得图象关于![]() 轴对称.其中所有正确结论的编号是( )
轴对称.其中所有正确结论的编号是( )
A.①②④B.①②C.③④D.②④
科目:高中数学 来源: 题型:
【题目】某学校高三年级有学生1000名,经调查,其中750名同学经常参加体育锻炼(称为![]() 类同学),另外250名同学不经常参加体育锻炼(称为
类同学),另外250名同学不经常参加体育锻炼(称为![]() 类同学),现用分层抽样方法(按
类同学),现用分层抽样方法(按![]() 类、
类、![]() 类分两层)从该年级的学生中共抽取100名同学,如果以身高达
类分两层)从该年级的学生中共抽取100名同学,如果以身高达![]() 作为达标的标准,对抽取的100名学生,得到以下列联表:
作为达标的标准,对抽取的100名学生,得到以下列联表:
身高达标 | 身高不达标 | 总计 | |
经常参加体育锻炼 | 40 | ||
不经常参加体育锻炼 | 15 | ||
总计 | 100 |
(Ⅰ)完成上表;
(Ⅱ)能否在犯错误的概率不超过0.05的前提下认为经常参加体育锻炼与身高达标有关系(![]() 的观测值精确到0.001)?
的观测值精确到0.001)?
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,右焦点为圆
,右焦点为圆![]() 的圆心,且圆
的圆心,且圆![]() 截
截![]() 轴所得弦长为4.
轴所得弦长为4.
(1)求椭圆![]() 与圆
与圆![]() 的方程;
的方程;
(2)若直线![]() 与曲线
与曲线![]() ,
,![]() 都只有一个公共点,记直线
都只有一个公共点,记直线![]() 与圆
与圆![]() 的公共点为
的公共点为![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.

(1)用五点法画出这个函数在一个周期内的图像;(必须列表)
(2)求它的振幅、周期、初相、对称轴方程;
(3)说明此函数图象可由![]() 在
在![]() 上的图象经过怎样的变换得到.
上的图象经过怎样的变换得到.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,直线l的参数方程为 (其中t为参数).现以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ=6cosθ.
(其中t为参数).现以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ=6cosθ.
(Ⅰ)写出直线l普通方程和曲线C的直角坐标方程;
(Ⅱ)过点M(-1,0)且与直线l平行的直线l1交C于A,B两点,求|AB|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,有一矩形钢板ABCD缺损了一角(如图所示),边缘线OM上每一点到点D的距离都等于它到边AB的距离.工人师傅要将缺损的一角切割下来使剩余部分成一个五边形,若AB=1m,AD=0.5m,则五边形ABCEF的面积最大值为____m2.

查看答案和解析>>
科目:高中数学 来源: 题型:
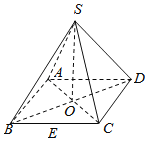
【题目】如图,四棱锥![]() 中,底面是边长为
中,底面是边长为![]() 的正方形ABCD,AC与BD的交点为O,
的正方形ABCD,AC与BD的交点为O,![]() 平面ABCD且
平面ABCD且![]() ,E是边BC的中点,动点P在四棱锥表面上运动,并且总保持
,E是边BC的中点,动点P在四棱锥表面上运动,并且总保持![]() ,则动点P的轨迹的周长为( )
,则动点P的轨迹的周长为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com