
【题目】已知函数![]() ,
,![]() .
.
(I)求证:![]() 在区间
在区间![]() 上单调递增;
上单调递增;
(II)若![]() ,函数
,函数![]() 在区间
在区间![]() 上的最大值为
上的最大值为![]() ,求
,求![]() 的试题分析式.并判断
的试题分析式.并判断![]() 是否有最大值和最小值,请说明理由(参考数据:
是否有最大值和最小值,请说明理由(参考数据:![]() )
)
【答案】(I)证明见解析;(II)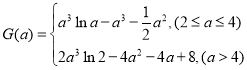
![]() 有最小值,没有最大值.
有最小值,没有最大值.
【解析】
试题分析:(Ⅰ)求出![]() 的导数,设
的导数,设![]() ,求出
,求出![]() 的导数,运用单调性即可得证;(Ⅱ)求出
的导数,运用单调性即可得证;(Ⅱ)求出![]() 的导数,求得单调区间,极值和当
的导数,求得单调区间,极值和当![]() 时,
时,![]() 时的最大值,结合零点存在定理,以及函数的单调性即可判断
时的最大值,结合零点存在定理,以及函数的单调性即可判断![]() 有最小值,没有最大值.
有最小值,没有最大值.
试题解析:(I)证明:∵![]() ,
,
∴![]() ,
,
设![]() ,则
,则![]() ,
,
∴当![]() 时,
时,![]() ,∴
,∴![]() 在区间
在区间![]() 上单调递增.
上单调递增.
∵![]() ,
,
∴当![]() 时,
时,![]() .
.
∴![]() 在区间
在区间![]() 上单调递增.
上单调递增.
(II)∵![]() ,
,
∴![]() 的定义域是
的定义域是![]() ,且
,且![]() ,即
,即![]() .
.
∵![]() ,∴
,∴![]() ,
,
当![]() 变化时,
变化时,![]() 、
、![]() 变化情况如下表:
变化情况如下表:

∴当![]() 时,
时,![]() ,
,![]() 在区间
在区间![]() 上的最大值是
上的最大值是![]() .
.
当![]() 时,
时,![]() 在区间
在区间![]() 上的最大值为
上的最大值为![]() .
.
即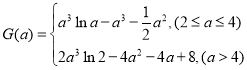 .
.
(1)当![]() 时,
时,![]() .
.
由(I)知,![]() 在
在![]() 上单调递增.
上单调递增.
又![]() ,
,![]() ,
,
∴存在唯一![]() ,使得
,使得![]() ,且当
,且当![]() 时,
时,![]() ,
,![]() 单调递减,当
单调递减,当![]() 时,
时,![]() ,
,![]() 单调递增.
单调递增.
∴当![]() 时,
时,![]() 有最小值
有最小值![]() .
.
(2)当![]() 时,
时,![]() ,
,
∴![]() 在
在![]() 单调递增.
单调递增.
又![]() ,
,
∴当![]() 时,
时,![]() .
.
∴![]() 在
在![]() 上单调递增.
上单调递增.
综合(1)(2)及![]() 试题分析式可知,
试题分析式可知,![]() 有最小值,没有最大值.
有最小值,没有最大值.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】随机询问某大学40名不同性别的大学生在购买食物时是否读营养说明,得到如下列联表:
性别与读营养说明列联表:
男 | 女 | 总计 | |
读营养说明 | 16 | 8 | 24 |
不读营养说明 | 4 | 12 | 16 |
总计 | 20 | 20 | 40 |
(Ⅰ)根据以上列联表进行独立性检验,能否在犯错误的概率不超过0.01的前提下认为性别与是否读营养说明之间有关系?
(Ⅱ)从被询问的16名不读营养说明的大学生中,随机抽取2名学生,求抽到男生人数![]() 的分布列及其均值(即数学期望).
的分布列及其均值(即数学期望).
(注:![]() ,其中
,其中![]() 为样本容量.)
为样本容量.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2009年推出一种新型家用轿车,购买时费用为![]() 万元,每年应交付保险费、养路费及汽油费共
万元,每年应交付保险费、养路费及汽油费共![]() 万元,汽车的维修费为:第一年无维修费用,第二年为
万元,汽车的维修费为:第一年无维修费用,第二年为![]() 万元,从第三年起,每年的维修费均比上一年增加
万元,从第三年起,每年的维修费均比上一年增加![]() 万元.(1)设该辆轿车使用
万元.(1)设该辆轿车使用![]() 年的总费用(包括购买费用、保险费、养路费、汽油费及维修费)为
年的总费用(包括购买费用、保险费、养路费、汽油费及维修费)为![]() ,求
,求![]() 的表达式;(2)这种汽车使用多少年报废最合算(即该车使用多少年,年平均费用最少)?
的表达式;(2)这种汽车使用多少年报废最合算(即该车使用多少年,年平均费用最少)?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正三棱柱![]() (侧棱垂直于底面,且底面是正三角形)中,
(侧棱垂直于底面,且底面是正三角形)中,![]() 是棱
是棱![]() 上一点.
上一点.
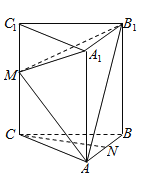
(1)若![]() 分别是
分别是![]() 的中点,求证:
的中点,求证:![]() 平面
平面![]() ;
;
(2)若![]() 是
是![]() 上靠近点
上靠近点![]() 的一个三等分点,求二面角
的一个三等分点,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com