
【题目】对于函数![]() ,若函数
,若函数![]() 是增函数,则称函数
是增函数,则称函数![]() 具有性质A.
具有性质A.
![]() 若
若![]() ,求
,求![]() 的解析式,并判断
的解析式,并判断![]() 是否具有性质A;
是否具有性质A;
![]() 判断命题“减函数不具有性质A”是否真命题,并说明理由;
判断命题“减函数不具有性质A”是否真命题,并说明理由;
![]() 若函数
若函数![]() 具有性质A,求实数k的取值范围,并讨论此时函数
具有性质A,求实数k的取值范围,并讨论此时函数![]() 在区间
在区间![]() 上零点的个数.
上零点的个数.
【答案】(1)![]() ,具有性质A;(2)假命题;(3)详见解析.
,具有性质A;(2)假命题;(3)详见解析.
【解析】
![]() 由
由![]() ,结合
,结合![]() 即可得出
即可得出![]() 解析式,和
解析式,和![]() 单调性,进而可得出结果;
单调性,进而可得出结果;
![]() 判断命题“减函数不具有性质A”,为假命题,举出反例即可,如
判断命题“减函数不具有性质A”,为假命题,举出反例即可,如![]() ;
;
![]() 若函数
若函数![]() 具有性质A,可知
具有性质A,可知![]() 在
在![]() 为增函数,进而可求出实数k的取值范围;再令
为增函数,进而可求出实数k的取值范围;再令![]() ,则
,则![]() 在区间
在区间![]() 上零点的个数,即是
上零点的个数,即是![]() 的根的个数,结合k的取值范围,即可求出结果.
的根的个数,结合k的取值范围,即可求出结果.
解:![]() ,
,![]() ,
,
![]() 在R上递增,可知
在R上递增,可知![]() 具有性质A;
具有性质A;
![]() 命题“减函数不具有性质A”,为假命题,比如:
命题“减函数不具有性质A”,为假命题,比如:![]() ,
,
![]() 在R上递增,
在R上递增,![]() 具有性质A;
具有性质A;
![]() 若函数
若函数![]() 具有性质A,
具有性质A,
可得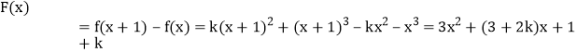
在![]() 递增,可得
递增,可得![]() ,解得
,解得![]() ;
;
由![]() ,可得
,可得![]() ,即
,即![]() ,
,
可得![]() ,
,![]() 时显然成立;
时显然成立;
![]() 时,
时,![]() ,
,
由![]() 在
在![]() 递减,且值域为
递减,且值域为![]() ,
,
![]() 时,
时,![]() 或1,
或1,![]() 有三解,3个零点;
有三解,3个零点;
当![]() 时,
时,![]() ,即
,即![]() ,可得
,可得![]() ,1个零点;
,1个零点;
当![]() 时,
时,![]() ,t有一解,x两解,即两个零点;
,t有一解,x两解,即两个零点;
当![]() ,且
,且![]() 时,
时,![]() 无解,即x无解,无零点.
无解,即x无解,无零点.


科目:高中数学 来源: 题型:
【题目】如图,过顶点在原点、对称轴为![]() 轴的抛物线
轴的抛物线![]() 上的点
上的点![]() 作斜率分别为
作斜率分别为![]() ,
,![]() 的直线,分别交抛物线
的直线,分别交抛物线![]() 于
于![]() ,
,![]() 两点.
两点.

(1)求抛物线![]() 的标准方程和准线方程;
的标准方程和准线方程;
(2)若![]() ,证明:直线
,证明:直线![]() 恒过定点.
恒过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
平面直角坐标系![]() 中,射线
中,射线![]() :
:![]() ,曲线
,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),曲线
为参数),曲线![]() 的方程为
的方程为![]() ;以原点为极点,
;以原点为极点,![]() 轴的非负半轴为极轴建立极坐标系.曲线
轴的非负半轴为极轴建立极坐标系.曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)写出射线![]() 的极坐标方程以及曲线
的极坐标方程以及曲线![]() 的普通方程;
的普通方程;
(Ⅱ)已知射线![]() 与
与![]() 交于
交于![]() ,
,![]() ,与
,与![]() 交于
交于![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班级的全体学生平均分成![]() 个小组,且每个小组均有
个小组,且每个小组均有![]() 名男生和多名女生.现从各个小组中随机抽取一名同学参加社区服务活动,若抽取的
名男生和多名女生.现从各个小组中随机抽取一名同学参加社区服务活动,若抽取的![]() 名学生中至少有一名男生的概率为
名学生中至少有一名男生的概率为![]() ,则( )
,则( )
A.该班级共有![]() 名学生
名学生
B.第一小组的男生甲被抽去参加社区服务的概率为![]()
C.抽取的![]() 名学生中男女生数量相同的概率是
名学生中男女生数量相同的概率是![]()
D.设抽取的![]() 名学生中女生数量为
名学生中女生数量为![]() ,则
,则![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将![]() 方格表任意一个角上的
方格表任意一个角上的![]() 小方格表挖去,剩下的图形称为“角形”.现在
小方格表挖去,剩下的图形称为“角形”.现在![]() 方格表中放置一些两两不重叠的角形,要求角形的边界与方格表的边界或分格线重合.求正整数
方格表中放置一些两两不重叠的角形,要求角形的边界与方格表的边界或分格线重合.求正整数![]() 的最大值,使得无论以何种方式放置了
的最大值,使得无论以何种方式放置了![]() 个角形之后,总能在方格表中再放入一个完整的角形.
个角形之后,总能在方格表中再放入一个完整的角形.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】港珠澳大桥是中国建设史上里程最长,投资最多,难度最大的跨海桥梁项目,大桥建设需要许多桥梁构件。从某企业生产的桥梁构件中抽取![]() 件,测量这些桥梁构件的质量指标值,由测量结果得到如图所示的频率分布直方图,质量指标值落在区间
件,测量这些桥梁构件的质量指标值,由测量结果得到如图所示的频率分布直方图,质量指标值落在区间![]() ,
,![]() ,
,![]() 内的频率之比为
内的频率之比为![]() .
.

(1)求这些桥梁构件质量指标值落在区间![]() 内的频率;
内的频率;
(2)若将频率视为概率,从该企业生产的这种桥梁构件中随机抽取![]() 件,记这
件,记这![]() 件桥梁构件中质量指标值位于区间
件桥梁构件中质量指标值位于区间![]() 内的桥梁构件件数为
内的桥梁构件件数为![]() ,求
,求![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com