
【题目】已知函数![]() 在
在![]() 处有极值
处有极值![]() .
.
(1)求![]() 的解析式;
的解析式;
(2)若关于![]() 的不等式
的不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)由题意得出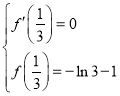 可得出关于
可得出关于![]() 、
、![]() 的方程组,解出这两个量的值,进而可求得函数
的方程组,解出这两个量的值,进而可求得函数![]() 的解析式;
的解析式;
(2)构造函数![]() ,由题意可知,不等式
,由题意可知,不等式![]() 对任意的
对任意的![]() 恒成立,求出导数
恒成立,求出导数![]() ,对实数
,对实数![]() 进行分类讨论,分析函数
进行分类讨论,分析函数![]() 在区间
在区间![]() 上的单调性,求出其最大值
上的单调性,求出其最大值![]() ,通过解不等式
,通过解不等式![]() 可求得实数
可求得实数![]() 的取值范围.
的取值范围.
(1)![]() ,
,![]() ,
,
因为函数![]() 在
在![]() 处有极值
处有极值![]() ,
,
得![]() ,
,![]() ,解得
,解得![]() ,
,![]() ,
,
所以![]() ;
;
(2)不等式![]() 恒成立,
恒成立,
即不等式![]() 恒成立,
恒成立,
令![]() ,
,
则不等式![]() 对任意的
对任意的![]() 恒成立,则
恒成立,则![]() .
.
![]() .
.
又![]() 函数
函数![]() 的定义域为
的定义域为![]() .
.
①当![]() 时,对任意的
时,对任意的![]() ,
,![]() ,则函数
,则函数![]() 在
在![]() 上单调递增.
上单调递增.
又![]() ,所以不等式
,所以不等式![]() 不恒成立;
不恒成立;
②当![]() 时,
时,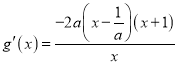 .
.
令![]() ,得
,得![]() ,当
,当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
因此,函数![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
故函数![]() 的最大值为
的最大值为![]() ,由题意得需
,由题意得需![]() .
.
令![]() ,
,![]() 函数
函数![]() 在
在![]() 上单调递减,
上单调递减,
又![]() ,由
,由![]() ,得
,得![]() ,
,![]() ,
,
因此,实数![]() 的取值范围是
的取值范围是![]() ;
;


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案科目:高中数学 来源: 题型:
【题目】(14分)已知a,b为常数,且a≠0,函数f(x)=﹣ax+b+axlnx,f(e)=2(e=2.71828…是自然对数的底数).
(I)求实数b的值;
(II)求函数f(x)的单调区间;
(III)当a=1时,是否同时存在实数m和M(m<M),使得对每一个t∈[m,M],直线y=t与曲线y=f(x)(x∈[![]() ,e])都有公共点?若存在,求出最小的实数m和最大的实数M;若不存在,说明理由.
,e])都有公共点?若存在,求出最小的实数m和最大的实数M;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在长方![]() 中,
中,![]() ,
,![]() ,E为
,E为![]() 的中点,以
的中点,以![]() 为折痕,把
为折痕,把![]() 折起到
折起到![]() 的位置,且平面
的位置,且平面![]() 平面
平面![]() .
.

(1)求证:![]() ;
;
(2)在棱![]() 上是否存在一点P,使得
上是否存在一点P,使得![]() 平面
平面![]() ,若存在,求出点P的位置,若不存在,请说明理由.
,若存在,求出点P的位置,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列事件A,B是独立事件的是( )
A. 一枚硬币掷两次,A=“第一次为正面向上”,B=“第二次为反面向上”
B. 袋中有两个白球和两个黑球,不放回地摸两球,A=“第一次摸到白球”,B=“第二次摸到白球”
C. 掷一枚骰子,A=“出现点数为奇数”,B=“出现点数为偶数”
D. A=“人能活到20岁”,B=“人能活到50岁”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》卷五《商功》中有如下叙述“今有刍甍,下广三丈,袤四丈,上袤二丈,无广,高一丈“刍甍”指的是底面为矩形的对称型屋脊状的几何体,“下广三丈”是指底面矩形宽三丈,“袤四丈”是指底面矩形长四丈,“上袤二丈”是指脊长二丈,“无宽”是指脊无宽度,“高一丈”是指几何体的高为一丈.现有一个刍甍如图所示,下广三丈,袤四丈,上袤三丈,无广,高二丈,则该刍甍的外接球的表面积为_______________平方丈.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com