
【题目】如图,在多面体ABCDE中,![]() ,
,![]() 平面ABC,
平面ABC,![]() ,
,![]() ,F为BC的中点,且
,F为BC的中点,且![]() .
.

(1)求证:![]() 平面ADF;
平面ADF;
(2)求二面角![]() 的正切值.
的正切值.
【答案】(1)见解析;(2)![]()
【解析】
(1)先证![]() ,
,![]() ,证AF⊥平面CDEB,得EF⊥AF,又EF⊥AD,从而EF⊥平面ADF;
,证AF⊥平面CDEB,得EF⊥AF,又EF⊥AD,从而EF⊥平面ADF;
(2)过点F作FH⊥AD,垂足为H,连接EH,可得∠EHF为二面角EADF的平面角,然后求出EF和FH,即可求出正切值.
解:(1)因为![]() 平面ABC,所以
平面ABC,所以![]() ,
,
因为![]() ,F为BC的中点,
,F为BC的中点,
所以![]() ,又
,又![]() ,
,
所以![]() 平面CDEB,
平面CDEB,
所以![]() ,又因为
,又因为![]() ,且
,且![]() ,
,
所以![]() 平面ADF.
平面ADF.
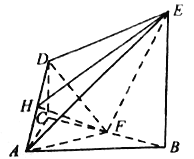
(2)过点F作![]() ,垂足为H,连接EH
,垂足为H,连接EH
由(1)知![]() ,
,
所以![]() 为二面角E-AD-F的平面角,
为二面角E-AD-F的平面角,
因为![]() ,F为BC的中点,
,F为BC的中点,
所以![]()
因为![]() ,
,![]() 平面ABC,
平面ABC,
所以![]() 平面ABC,
平面ABC,![]() ,
,![]()
所以![]()
由(1)知![]() ,所以
,所以![]() ,
,
所以![]() ,所以
,所以![]()
因为![]() ,
,
所以![]() ,所以
,所以![]() ,
,
因为![]() 平面CDEB,所以
平面CDEB,所以![]() ,所以
,所以![]()
由等面积法得![]() ,
,
所以![]() ,
,
所以二面角E-AD-F的正切值为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知点![]() ,点
,点![]() 是圆
是圆![]() 上的任意一点,设
上的任意一点,设![]() 为该圆的圆心,并且线段
为该圆的圆心,并且线段![]() 的垂直平分线与直线
的垂直平分线与直线![]() 交于点
交于点![]() .
.
(1)求点![]() 的轨迹方程;
的轨迹方程;
(2)已知![]() 两点的坐标分别为
两点的坐标分别为![]() ,
, ![]() ,点
,点![]() 是直线
是直线![]() 上的一个动点,且直线
上的一个动点,且直线![]() 分别交(1)中点
分别交(1)中点![]() 的轨迹于
的轨迹于![]() 两点(
两点(![]() 四点互不相同),证明:直线
四点互不相同),证明:直线![]() 恒过一定点,并求出该定点坐标.
恒过一定点,并求出该定点坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
在直角坐标系中,以原点为极点,![]() 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线![]() :
:![]() ,过点
,过点![]() 的直线
的直线![]() 的参数方程为:
的参数方程为:![]() (
(![]() 为参数),直线
为参数),直线![]() 与曲线
与曲线![]() 分别交于
分别交于![]() 、
、![]() 两点.
两点.
(1)写出曲线![]() 的直角坐标方程和直线
的直角坐标方程和直线![]() 的普通方程;
的普通方程;
(2)求线段![]() 的长和
的长和![]() 的积.
的积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国是世界上严重缺水的国家,某市为了制定合理的节水方案,对居民用水情况进行调查,通过抽样,获得某年100为居民每人的月均用水量(单位:吨),将数据按照![]() 分成9组,制成了如图所示的频率分布直方图.
分成9组,制成了如图所示的频率分布直方图.
(1)求直方图的![]() 的值;
的值;
(2)设该市有30万居民,估计全市居民中月均用水量不低于3吨的人数,说明理由.
(3)估计居民月用水量的中位数.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】天坛公园是明、清两代皇帝“祭天”“祈谷”的场所.天坛公园中的圜丘台共有三层(如图1所示),上层坛的中心是一块呈圆形的大理石板,从中心向外围以扇面形石(如图2所示).上层坛从第一环至第九环共有九环,中层坛从第十环至第十八环共有九环,下层坛从第十九环至第二十七环共有九环;第一环的扇面形石有9块,从第二环起,每环的扇面形石块数比前一环多9块,则第二十七环的扇面形石块数是______;上、中、下三层坛所有的扇面形石块数是_______.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面立角坐标系![]() 中,过点
中,过点![]() 的圆的圆心
的圆的圆心![]() 在
在![]() 轴上,且与过原点倾斜角为
轴上,且与过原点倾斜角为![]() 的直线
的直线![]() 相切.
相切.
(1)求圆![]() 的标准方程;
的标准方程;
(2)点![]() 在直线
在直线![]() 上,过点
上,过点![]() 作圆
作圆![]() 的切线
的切线![]() 、
、![]() ,切点分别为
,切点分别为![]() 、
、![]() ,求经过
,求经过![]() 、
、![]() 、
、![]() 、
、![]() 四点的圆所过的定点的坐标.
四点的圆所过的定点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com