
����Ŀ��Ϊ����������ij��λ�����¹��գ��Ѷ�����̼ת��Ϊһ�ֿ����õĻ�����Ʒ����֪�õ�λÿ�µĴ�����������300�֣��´����ɱ�![]() ��Ԫ�����´�����
��Ԫ�����´�����![]() ���֣�֮��ĺ�����ϵʽ�ɽ��Ƶı�ʾΪ��
���֣�֮��ĺ�����ϵʽ�ɽ��Ƶı�ʾΪ��![]() ����ÿ����һ�ֶ�����̼�õ������õĻ�����Ʒ��ֵΪ300Ԫ��
����ÿ����һ�ֶ�����̼�õ������õĻ�����Ʒ��ֵΪ300Ԫ��
��1���õ�λÿ�´�����Ϊ���ٶ�ʱ������ʹÿ�ֵ�ƽ�������ɱ���ͣ�
��2��Ҫ��֤�õ�λÿ�²�������ÿ�´�����Ӧ������ʲô��Χ��
���𰸡���1��![]() ʱ������ʹÿ�ֵ�ƽ�������ɱ���ͣ���2����
ʱ������ʹÿ�ֵ�ƽ�������ɱ���ͣ���2����![]() ʱ���õ�λÿ�²�����.
ʱ���õ�λÿ�²�����.
��������
(1) ������̼��ÿ��ƽ�������ɱ�Ϊ![]() ,�ɾ�ֵ����ʽ��ý������2��
,�ɾ�ֵ����ʽ��ý������2��![]() ��϶��κ����������Լ�����õ����.
��϶��κ����������Լ�����õ����.
��1���������֪��������̼��ÿ��ƽ�������ɱ�Ϊ![]()
��Ϊ![]() �����ҽ���
�����ҽ���![]() ����
����![]() ʱ������ʹÿ�ֵ�ƽ�������ɱ����;
ʱ������ʹÿ�ֵ�ƽ�������ɱ����;
��2����õ�λÿ�»���ΪS��Ԫ������
![]()
��![]() ,
,
�������֪![]() �����Ե�
�����Ե�![]() ʱ���õ�λÿ�²�����.
ʱ���õ�λÿ�²�����.


 С��ʿ��ĩ����100��ϵ�д�
С��ʿ��ĩ����100��ϵ�д� ��У��ʦ������ҵ���Ӻ����Ծ�ϵ�д�
��У��ʦ������ҵ���Ӻ����Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ������
������![]() ������
������
��1����![]() �ĵ��������䣻
�ĵ��������䣻
��2����![]() ʱ��
ʱ��![]() �����ֵΪ
�����ֵΪ![]() ����
����![]() ��ֵ��
��ֵ��
��3����![]() ȡ���ֵʱ
ȡ���ֵʱ![]() ��ȡֵ����.
��ȡֵ����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]()
��1������![]() ����С�����ڡ��������䣻
����С�����ڡ��������䣻
��2������![]() ������
������![]() �ϵ���Сֵ�����ֵ.
�ϵ���Сֵ�����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��������ABC��A1B1C1�У�����AA1�͵���A1B1C1��AA1��1������������A1B1C1�DZ߳�Ϊ2���������Σ�E��BC�е㣬������˵����ȷ���ǣ� ��

��CC1��AB1���ɽǵ�����ֵΪ![]()
��AB��ƽ��ACC1A1
��������AB1EΪֱ��������
��A1C1��ƽ��AB1E
A.�٢�B.�ۢ�C.�٢�D.�ڢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
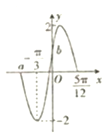
����Ŀ������f��x��=Asin��2��x+�գ���A��0���أ�0��|��|��![]() ���IJ���ͼ����ͼ��ʾ
���IJ���ͼ����ͼ��ʾ
��1����A���أ��յ�ֵ��
��2����ͼ��a��b��ֵ������f��x���ĵ������䣻
��3��������[0����]����f������=![]() �������ֵ��
�������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ��Բ����뾶Ϊ![]() ����Ϊ
����Ϊ![]() ��
��
��1����Բ�ı����.
��2����Բ���ڽ�������������������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��5������3��Ů���μ�������ʽ��
��1��վ�����ţ�3��Ů��վǰ�ţ�5������վ�����ж�����վ����
��2��վ�����У�ÿ��4�ˣ�ÿ�ж���Ů����Ů��վ������ǰ�棬�ж��������з�����
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com