
【题目】已知四棱锥S﹣ABCD的底面ABCD是正方形,SA⊥底面ABCD,E是SC上的任意一点.过点E的平面α垂直于平面SAC. 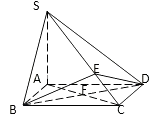
(1)请作出平面α截四棱锥S﹣ABCD的截面(只需作图并写出作法);
(2)当SA=AB时,求二面角B﹣SC﹣D的大小.
【答案】
(1)解:∵SA⊥底面ABCD,∴SA⊥BD,
∵底面ABCD是正方形,∴BD⊥AC,
则BD⊥平面SAC,
若点E的平面α垂直于平面SAC,
则平面α 与底面的交线平行于BD即可.

(2)解:如图所示建立空间直角坐标系,
点A为坐标原点,AB,AD,AS所在的直线分别为x,y,z轴.设AB=1.
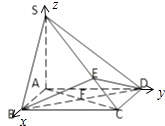
由题意得B(1,0,0),S(0,0,1),C(1,1,0),D(0,1,0),
![]() =(1,0,﹣1),又
=(1,0,﹣1),又 ![]() =(1,1,﹣1)
=(1,1,﹣1)
设平面BSC的法向量为 ![]() (x1,y1,z1),则
(x1,y1,z1),则
 ,令z1=1,则
,令z1=1,则 ![]() =(1,0,1,
=(1,0,1,
![]() =(0,﹣1,1)
=(0,﹣1,1) ![]() =(1,0,0),
=(1,0,0),
设平面SCD的法向量为 ![]() =(x2,y2,z2),则
=(x2,y2,z2),则
 ,令y2=1,则
,令y2=1,则 ![]() =(0,1,1),
=(0,1,1),
设二面角B﹣SC﹣D的平面角为α,则
|cosα|=  =
= ![]() =
= ![]() .
.
显然二面角B﹣SC﹣D的平面角为α为钝角,所以α=120°,
即二面角C﹣PB﹣D的大小为120°
【解析】(1)根据条件先证明BD⊥平面SAC,则面α 与底面的交线平行于BD即可;(2)建立空间直角坐标系,求出平面BSC、平面SCD的法向量,利用向量的夹角公式,即可求二面角B﹣SC﹣D的大小.
【考点精析】通过灵活运用平面与平面垂直的性质,掌握两个平面垂直,则一个平面内垂直于交线的直线与另一个平面垂直即可以解答此题.


科目:高中数学 来源: 题型:
【题目】椭圆 ![]() 的左右焦点分别为F1 , F2 , 离心率为
的左右焦点分别为F1 , F2 , 离心率为 ![]() ,过点F1且垂直于x轴的直线被椭圆截得的弦长为
,过点F1且垂直于x轴的直线被椭圆截得的弦长为 ![]() ,直线l:y=kx+m与椭圆交于不同的A,B两点.
,直线l:y=kx+m与椭圆交于不同的A,B两点.
(1)求椭圆C的方程;
(2)若在椭圆C上存在点Q满足: ![]() (O为坐标原点).求实数λ的取值范围.
(O为坐标原点).求实数λ的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校拟在广场上建造一个矩形花园,如图所示,中间是完全相同的两个椭圆型花坛,每个椭圆型花坛的面积均为216π平方米,两个椭圆花坛的距离是1.5米.整个矩形花坛的占地面积为S.
(注意:椭圆面积为πab,其中a,b分别为椭圆的长短半轴长)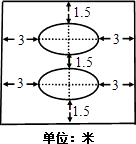
(1)根据图中所给数据,试用a、b表示S;
(2)当椭圆形花坛的长轴长为多少米时,所建矩形花园占地最少?并求出最小面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2+bx+3a+b是偶函数,且其定义域为[a﹣1,2a],则( )
A.![]() ,b=0
,b=0
B.a=﹣1,b=0
C.a=1,b=1
D.a= ![]() ,b=﹣1
,b=﹣1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+2ax+2,x∈[﹣5,5],
(1)当a=﹣1时,求函数的最大值和最小值;
(2)求实数a的取值范围,使y=f(x)在区间[﹣5,5]上是单调减函数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正四棱锥S﹣ABCD中,O为顶点在底面内的投影,P为侧棱SD的中点,且SO=OD,则直线BC与平面PAC的夹角是( )
A.30°
B.45°
C.60°
D.75°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于二次函数y=﹣4x2+8x﹣3,
(1)指出图象的开口方向、对称轴方程、顶点坐标;
(2)求函数的最大值或最小值;
(3)写出函数的单调区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数y=f(x)的定义域是[0,2],则函数y=f(2x﹣1)的定义域是( )
A.{x|0≤x≤1}
B.{x|0≤x≤2}
C.{x| ![]() ≤x≤
≤x≤ ![]() }
}
D.{x|﹣1≤x≤3}
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com