
【题目】定义在D上的函数f(x),如果满足:对任意x∈D,存在常数M>0,都有|f(x)|≤M成立,则称f(x)是D上的有界函数,其中M称为函数f(x)的上界.已知函数 ![]() .
.
(1)若f(x)是奇函数,求m的值;
(2)当m=1时,求函数f(x)在(﹣∞,0)上的值域,并判断函数f(x)在(﹣∞,0)上是否为有界函数,请说明理由;
(3)若函数f(x)在[0,1]上是以3为上界的函数,求实数m的取值范围.
【答案】
(1)解:由f(x)是奇函数,则f(﹣x)=﹣f(x)
得 ![]() ,即(1﹣m2)2x=0,∴m2﹣1=0,m=±1
,即(1﹣m2)2x=0,∴m2﹣1=0,m=±1
(2)解:当m=1时, ![]() .
.
∵x<0,∴0<2x<1,∴f(x)∈(0,1),满足|f(x)|≤1.
∴f(x)在(﹣∞,0)上为有界函数
(3)解:若函数f(x)在[0,1]上是以3为上界的有界函数,则有|f(x)|≤3在[0,1]上恒成立.
∴﹣3≤f(x)≤3,
即 ![]() ,
,
∴ 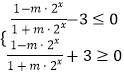 ,化简得:
,化简得:  ,
,
即 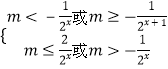 ,
,
上面不等式组对一切x∈[0,1]都成立,
故  ,
,
∴ ![]()
【解析】(1)根据函数奇偶性的性质建立方程关系进行求解即可.(2)根据分式函数的性质以及有界函数的定义进行求解判断即可.(3)根据函数的有界性建立不等式关系,利用不等式恒成立进行求解即可.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)= 
(1)当x≤0时,解不等式f(x)≥﹣1;
(2)写出该函数的单调区间;
(3)若函数g(x)=f(x)﹣m恰有3个不同零点,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
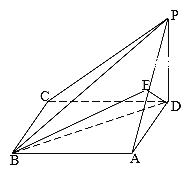
【题目】如图,四棱锥P-ABCD中,底面ABCD为矩形,PD垂直于底面ABCD,AD=PD,E分别为AP的中点.
(Ⅰ)求证:DE垂直于平面PAB;
(Ⅱ)设BC =![]() ,AB=2,求直线EB与平面ABD所成的角的大小.
,AB=2,求直线EB与平面ABD所成的角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数f(x)定义域中任意的x1 , x2(x1≠x2)有如下结论
1)f(x1+x2)=f(x1)f(x2)
2)f(x1x2)=f(x1)+f(x2)
3) ![]() >0
>0
4)f( ![]() )<
)< ![]()
5)f( ![]() )>
)> ![]()
6)f(﹣x)=f(x).
当f(x)=lgx时,上述结论正确的序号为 . (注:把你认为正确的命题的序号都填上).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知p:关于x的不等式x2+2ax+4>0对一切 ![]() 恒成立;q:函数f(x)=-(5-2a)x在R上是减函数.若“p或q”为真,“p且q”为假,求实数a的取值范围( )。
恒成立;q:函数f(x)=-(5-2a)x在R上是减函数.若“p或q”为真,“p且q”为假,求实数a的取值范围( )。
A.![]()
B.B、
C.C、
D.a≥-2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)是定义R上的偶函数,且当x∈[0,+∞)时,函数f(x)是单调递减函数,则f(log25),f(log3 ![]() ),f(log53)大小关系是( )
),f(log53)大小关系是( )
A.f(log3 ![]() )<f(log53)<f(log25)
)<f(log53)<f(log25)
B.f(log3 ![]() )<f(log25)<f(log53)
)<f(log25)<f(log53)
C.f(log53)<f(log3 ![]() )<f(log25)
)<f(log25)
D.f(log25)<f(log3 ![]() )<f(log53)
)<f(log53)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知关于x的不等式x2﹣(a2+3a+2)x+3a(a2+2)<0(a∈R).
(Ⅰ)解该不等式;
(Ⅱ)定义区间(m,n)的长度为d=n﹣m,若a∈R,求该不等式解集表示的区间长度的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学著作《九章算术》有如下问题:“今有蒲(水生植物名)生一日,长三尺;莞(植物名,俗称水葱、席子草)生一日,长一尺.蒲生日自半,莞生日自倍.问几何日而长等?”意思是:今有蒲生长1日,长为3尺;莞生长1日,长为1尺.蒲的生长逐日减半,莞的生长逐日增加1倍.若蒲、莞长度相等,则所需的时间约为( )(结果保留一位小数.参考数据:![]() ,
,![]() )( )
)( )
A. 1.3日 B. 1.5日 C. 2.6日 D. 2.8日
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lg(3+x)﹣lg(3﹣x)
(1)求f(x)的定义域;
(2)判断f(x)的奇偶性并证明;
(3)若f(a)=4,求f(﹣a)的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com