
设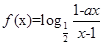 为奇函数,
为奇函数,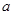 为常数,
为常数,
(1)求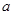 的值;
的值;
(2)证明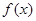 在区间
在区间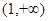 上单调递增;
上单调递增;
(3)若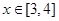 ,不等式
,不等式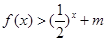 恒成立,求实数
恒成立,求实数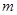 的取值范围。
的取值范围。
科目:高中数学 来源: 题型:解答题
已知函数 ,若f(x)在x=1处的切线方程为3x+y-6=0
,若f(x)在x=1处的切线方程为3x+y-6=0
(Ⅰ)求函数f(x)的解析式;
(Ⅱ)若对任意的 ,都有f(x)
,都有f(x) 成立,求函数g(t)
成立,求函数g(t)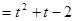 的最值
的最值
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知m∈R,对p:x1和x2是方程x2-ax-2=0的两个根,不等式|m-5|≤|x1-x2|对任意实数a∈[1,2]恒成立;q:函数f(x)=3x2+2mx+m+ 有两个不同的零点.求使“p且q”为假命题、“p或q”为真命题的实数m的取值范围.
有两个不同的零点.求使“p且q”为假命题、“p或q”为真命题的实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某地区注重生态环境建设,每年用于改造生态环境总费用为 亿元,其中用于风景区改造为
亿元,其中用于风景区改造为 亿元。该市决定建立生态环境改造投资方案,该方案要求同时具备下列三个条件:①每年用于风景区改造费用随每年改造生态环境总费用增加而增加;②每年改造生态环境总费用至少
亿元。该市决定建立生态环境改造投资方案,该方案要求同时具备下列三个条件:①每年用于风景区改造费用随每年改造生态环境总费用增加而增加;②每年改造生态环境总费用至少 亿元,至多
亿元,至多 亿元;③每年用于风景区改造费用不得低于每年改造生态环境总费用的15%,但不得每年改造生态环境总费用的22%。
亿元;③每年用于风景区改造费用不得低于每年改造生态环境总费用的15%,但不得每年改造生态环境总费用的22%。
(1)若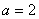 ,
, ,请你分析能否采用函数模型y=
,请你分析能否采用函数模型y=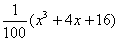 作为生态环境改造投资方案;
作为生态环境改造投资方案;
(2)若 、
、 取正整数,并用函数模型y=
取正整数,并用函数模型y=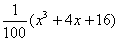 作为生态环境改造投资方案,请你求出
作为生态环境改造投资方案,请你求出 、
、 的取值.
的取值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
石家庄市为鼓励居民节约用电,采用分段计费的方法计算电费,每月用电不超过100度时,按每度0.52元计算,每月用电量超过100度时,其中的100度仍按原标准收费,超过的部分每度按0.6元计算.
(1)设月用电 度时,应缴电费
度时,应缴电费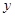 元,写出
元,写出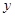 关于
关于 的函数关系式;
的函数关系式;
(2)小明家第一季度缴纳电费情况如下:
| 月份 | 一月 | 二月 | 三月 | 合计 |
| 缴费金额 | 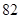 元 元 | 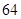 元 元 |  元 元 | 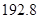 元 元 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
一边长为 的正方形铁片,铁片的四角截去四个边长均为
的正方形铁片,铁片的四角截去四个边长均为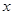 的小正方形,然后做成一个无盖方盒。
的小正方形,然后做成一个无盖方盒。
(1)试把方盒的容积 表示为
表示为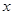 的函数;(2)
的函数;(2)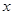 多大时,方盒的容积
多大时,方盒的容积 最大?
最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com