
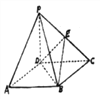
【题目】如图,四棱锥![]() 的底面
的底面![]() 是正方形,侧棱
是正方形,侧棱![]() 底面
底面![]() ,
, ![]() ,
, ![]() 是
是![]() 的中点.
的中点.
(1)求二面角![]() 的平面角的余弦值;
的平面角的余弦值;
(2)在被![]() 上是否存在点
上是否存在点![]() ,使
,使![]() 平面
平面![]() ?证明你的结论.
?证明你的结论.
【答案】(1)![]() ;(2)见解析.
;(2)见解析.
【解析】试题分析:(1)建立空间直角坐标系,分别求出两个平面的法向量,利用向量的有关运算计算出两个向量的夹角,进而得到二面角平面角的余弦值;(2)假设存在点![]() ,则直线
,则直线![]() 所在的向量与平面
所在的向量与平面![]() 的法向量平行,根据这个条件可得到一个方程,再根据有关知识判断方程的解的情况.
的法向量平行,根据这个条件可得到一个方程,再根据有关知识判断方程的解的情况.
试题解析:以![]() 为坐标原点,分别以
为坐标原点,分别以![]() ,
, ![]() ,
, ![]() 所在直线为
所在直线为![]() 轴、
轴、![]() 轴、
轴、![]() 轴建立空间直角坐标系,
轴建立空间直角坐标系,
则![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
所以![]() ,
, ![]() ,
, ![]() .
.

(1)设![]() 是平面
是平面![]() 的一个法向量,
的一个法向量,
则由 ,得
,得![]() ;取
;取![]() ,则
,则![]() ,
,
又![]() 是平面
是平面![]() 的一个法向量.设二面角
的一个法向量.设二面角![]() 的平面角为
的平面角为![]() ,
,

![]() ,二面角
,二面角![]() 为钝角,余弦值为
为钝角,余弦值为![]() .
.
(2)![]() ,
, ![]() ,
, ![]()
![]() ,
, ![]() .
.
假设棱![]() 上存在点
上存在点![]() ,使
,使![]() 平面
平面![]() ,设
,设![]() ,(
,( ![]() ),
),
则![]() ,
, ![]()
![]() ,
,
由![]() 得
得![]()
![]() ,
, ![]() ,此时
,此时![]() ,
,
即在棱![]() 上存在点
上存在点![]() ,
, ![]() ,使得
,使得![]() 平面
平面![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=elnx,g(x)=![]() f(x)-(x+1).(e=2.718……)
f(x)-(x+1).(e=2.718……)
(1)求函数g(x)的极大值;
(2)求证:1+![]() +
+![]() +…+
+…+![]() >ln(n+1)(n∈N*).
>ln(n+1)(n∈N*).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() ),将
),将![]() 的图象向左平移
的图象向左平移![]() 个单位长度后得到
个单位长度后得到![]() 的图象,且
的图象,且![]() 在区间
在区间![]() 内的最大值为
内的最大值为![]() .
.
(1)求实数![]() 的值;
的值;
(2)在![]() 中,内角
中,内角![]() ,
, ![]() ,
, ![]() 的对边分别是
的对边分别是![]() ,
, ![]() ,
, ![]() ,若
,若![]() ,且
,且![]() ,求
,求![]() 的周长
的周长![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种产品的广告费支出![]() 与销售额
与销售额![]() (单位:万元)之间有如下对应数据:
(单位:万元)之间有如下对应数据:
|
|
|
|
|
|
|
|
|
|
|
|
(1)求回归直线方程;
(2)试预测广告费支出为![]() 万元时,销售额多大?
万元时,销售额多大?
(3)在已有的五组数据中任意抽取两组,求至少有一组数据其预测值与实际值之差的绝对值不超过![]() 的概率.(参考数据:
的概率.(参考数据: 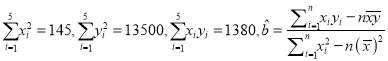 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了研究“教学方式”对教学质量的影响,某高中老师分别用两种不同的教学方式对入学数学平均分数和优秀率都相同的甲、乙两个高一新班进行教学(勤奋程度和自觉性都一样).以下茎叶图为甲、乙两班(每班均为20人)学生的数学期末考试成绩.

(1)现从甲班数学成绩不低于80分的同学中随机抽取两名同学,求成绩为87分的同学至少有一名被抽中的概率;
(2)学校规定:成绩不低于75分的为优秀,请填写下面的![]() 列联表,并判断有多大把握认为“成绩优秀与教学方式有关”.
列联表,并判断有多大把握认为“成绩优秀与教学方式有关”.
甲班 | 乙班 | 合计 | |
优秀 | |||
不优秀 | |||
合计 |
下面临界值表供参考:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| span>2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式:![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业接到生产3000台某产品的A,B,C三种部件的订单,每台产品需要这三种部件的数量分别为2,2,1(单位:件).已知每个工人每天可生产A部件6件,或B部件3件,或C部件2件.该企业计划安排200名工人分成三组分别生产这三种部件,生产B部件的人数与生产A部件的人数成正比,比例系数为k(k为正整数).
(1)设生产A部件的人数为x,分别写出完成A,B,C三种部件生产需要的时间;
(2)假设这三种部件的生产同时开工,试确定正整数k的值,使完成订单任务的时间最短,并给出时间最短时具体的人数分组方案.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com