
【题目】已知函数f(x)=ax2+bx+c(a>0,b∈R,c∈R).
(1)若函数f(x)的最小值是f(﹣1)=0,且c=1,求f (2)的值;
(2)若a=1,c=0,且|f(x)|≤1在区间(0,1]上恒成立,试求b的取值范围.
【答案】(1)9 ; (2)[﹣2,![]() ].
].
【解析】
(1)根据函数f(x)的最小值是f(﹣1)=0,且c=1,求解得a,b,即可求解f (2)的值;
(2)将a=1,c=0代入,|f(x)|≤1在区间(0,1]上恒成立,转化为不等式问题求解即可.
函数f(x)=ax2+bx+c(a>0,b∈R,c∈R).
(1)由题意,可得![]() ,a﹣b+1=0,
,a﹣b+1=0,
解得:a=1,b=2;
∴函数f(x)=x2+2x+1.
那么f(2)=4+4+1=9;
(2)由a=1,c=0,可得f(x)=x2+bx;
∵|f(x)|≤1在区间(0,1]上恒成立,
即|x2+bx|≤1
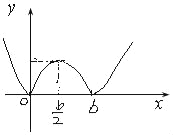
令g(x)=|x2+bx|=|x(x+b)|,显然图象过原点,(b,0).
当b<0,g(x)在区间(0,1]上单调递增,可得g(x)的图象,(如图)
g(x)max=g(1)=|b+1|≤1
∴﹣2≤b<0
当b=0时,可得|x2|≤1在区间(0,1]上恒成立,
可得:﹣2≤b≤0;
当b>0,显然g(x)max=![]()
解得:![]() ≥b>0
≥b>0
综上可得b的取值范围是[﹣2,![]() ].
].


 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:高中数学 来源: 题型:
【题目】在四棱锥P﹣ABCD中,平面四边形ABCD中AD∥BC,∠BAD为二面角B﹣PA﹣D一个平面角. 
(1)若四边形ABCD是菱形,求证:BD⊥平面PAC;
(2)若四边形ABCD是梯形,且平面PAB∩平面PCD=l,问:直线l能否与平面ABCD平行?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,经过点
中,经过点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 有两个不同的交点
有两个不同的交点![]() 和
和![]() .
.
(1)求![]() 的取值范围;
的取值范围;
(2)设椭圆与![]() 轴正半轴、
轴正半轴、![]() 轴正半轴的交点分别为
轴正半轴的交点分别为![]() ,是否存在常数
,是否存在常数![]() ,使得向量
,使得向量![]() 与
与![]() 共线?如果存在,求
共线?如果存在,求![]() 值;如果不存在,请说明理由.
值;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方体![]() 中,过对角线
中,过对角线![]() 的一个平面交
的一个平面交![]() 于点
于点![]() ,交
,交![]() 于
于![]() .
.
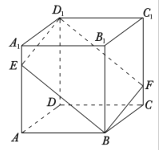
①四边形![]() 一定是平行四边形;
一定是平行四边形;
②四边形![]() 有可能是正方形;
有可能是正方形;
③四边形![]() 在底面
在底面![]() 内的投影一定是正方形;
内的投影一定是正方形;
④四边形![]() 有可能垂直于平面
有可能垂直于平面![]() .
.
以上结论正确的为_______________.(写出所有正确结论的编号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某居民区的物业部门每月向居民收取卫生费,计费方法如下:3人和3人以下的住户,每户收取5元;超过3人的住户,每超出1人加收1.2元.设计一个算法,根据输入的人数,计算应收取的卫生费,并画出程序框图.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com