
已知半径为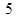 的圆的圆心在
的圆的圆心在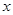 轴上,圆心的横坐标是整数,且与直线
轴上,圆心的横坐标是整数,且与直线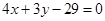 相切.
相切.
(Ⅰ)求圆的方程;
(Ⅱ)设直线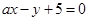
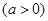 与圆相交于
与圆相交于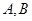 两点,求实数
两点,求实数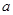 的取值范围;
的取值范围;
(Ⅲ)
在(Ⅱ)的条件下,是否存在实数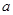 ,使得弦
,使得弦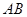 的垂直平分线
的垂直平分线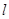 过点
过点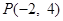 ,若存在,求出实数
,若存在,求出实数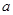 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(1)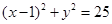 (2)
(2)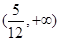 (3)
(3)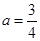
【解析】
试题分析:解:(Ⅰ)设圆心为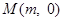 (
(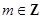 ).由于圆与直线
).由于圆与直线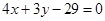 相切,且半径为
相切,且半径为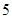 ,所以
,所以 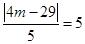 ,即
,即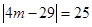 .因为
.因为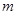 为整数,故
为整数,故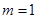 .
.
故所求圆的方程为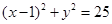 .
4分
.
4分
(Ⅱ)把直线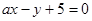 ,即
,即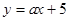 代入圆的方程,消去
代入圆的方程,消去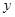 整理,得
整理,得
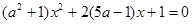
由于直线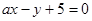 交圆于A、B两点,故
交圆于A、B两点,故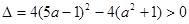
即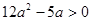 ,由于
,由于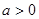 ,解得
,解得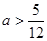
所以实数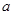 的取值范围
的取值范围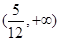
(Ⅲ)设符合条件的实数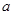 存在,由于,则直线
存在,由于,则直线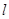 的斜率为
的斜率为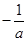
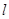 的方程为
的方程为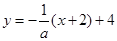 ,即
,即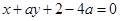
由于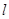 垂直平分弦AB,故圆心
垂直平分弦AB,故圆心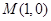 必在
必在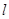 上,
上,
所以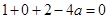 ,解得
,解得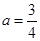 。由于
。由于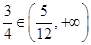 ,故存在实数
,故存在实数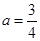
使得过点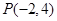 的直线
的直线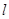 垂直平分弦AB
14分
垂直平分弦AB
14分
考点:直线与圆的位置关系
点评:解决的关键是利用直线与圆相切,结合点到直线的距离公式得到圆的方程,编辑和图像有交点,结合方程有实数根来得到,,属于基础题。


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:高中数学 来源:2014届福建省高一下学期第二次月考数学试卷(解析版) 题型:解答题
已知半径为 的圆的圆心在
的圆的圆心在 轴上,圆心的横坐标是整数,且与直线
轴上,圆心的横坐标是整数,且与直线 相切.
相切.
(1)求圆的方程;
(2)设直线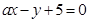
 与圆相交于
与圆相交于 两点,求实数
两点,求实数 的取值范围;
的取值范围;
(3) 在(Ⅱ)的条件下,是否存在实数 ,使得弦
,使得弦 的垂直平分线
的垂直平分线 过点
过点 ,若存在,求出实数
,若存在,求出实数 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2014届广东省高一5月月考数学试卷(解析版) 题型:解答题
(本题满分14分)
已知半径为 的圆的圆心在
的圆的圆心在 轴上,圆心的横坐标是整数,且与直线
轴上,圆心的横坐标是整数,且与直线 相切.
相切.
(1)求圆的方程;
(2)设直线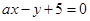
 与圆相交于
与圆相交于 两点,求实数
两点,求实数 的取值范围;
的取值范围;
(3) 在(2)的条件下,是否存在实数 ,使得弦
,使得弦 的垂直平分线
的垂直平分线 过点
过点 ,若存在,求出实数
,若存在,求出实数 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2014届福建省高一第三模块数学试卷(解析版) 题型:解答题
已知半径为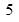 的圆的圆心在
的圆的圆心在 轴上,且与直线
轴上,且与直线 相切.圆心的横坐标是整数。
相切.圆心的横坐标是整数。
(1)求圆的方程;
(2)设直线
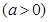 与圆相交于
与圆相交于 两点,求实数
两点,求实数 的取值范围;
的取值范围;
(3) 在(Ⅱ)的条件下,是否存在实数 ,使得弦
,使得弦 的垂直平分线
的垂直平分线 过点
过点 ,若存在,求出实数
,若存在,求出实数 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2014届福建省等五校高一第一学期期末联考数学 题型:解答题
(本小题满分14分)已知半径为 的圆的圆心在
的圆的圆心在 轴上,圆心的横坐标是整数,且与直线
轴上,圆心的横坐标是整数,且与直线 相切.
相切.
(Ⅰ)求圆的方程;
(Ⅱ)设直线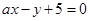
 与圆相交于
与圆相交于 两点,求实数
两点,求实数 的取值范围;
的取值范围;
(Ⅲ) 在(Ⅱ)的条件下,是否存在实数 ,使得弦
,使得弦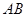 的垂直平分线
的垂直平分线 过点
过点 ,若存在,求出实数
,若存在,求出实数 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2014届福建省高一下学期第一次月考数学试卷 题型:解答题
已知半径为 的圆的圆心在
的圆的圆心在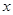 轴上,圆心的横坐标是整数,且与直线
轴上,圆心的横坐标是整数,且与直线 相切.
相切.
(Ⅰ)求圆的方程;
(Ⅱ)设直线
 与圆相交于
与圆相交于 两点,求实数
两点,求实数 的取值范围;
的取值范围;
(Ⅲ) 在(Ⅱ)的条件下,是否存在实数 ,使得弦
,使得弦 的垂直平分线
的垂直平分线 过点
过点 ,若存在,求出实数
,若存在,求出实数 的值;若不存在,请说明理由
的值;若不存在,请说明理由
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com